$10\,kg$ દળનો પદાર્થ $20\,m/s$ ના પ્રારંભિક વેગથી ગતિ કરે છે. પદાર્થ અને જમીન વચ્ચેના ઘર્ષણને કારણે પદાર્થ $5\,s$ પછી સ્થિર થાય છે. તો ઘર્ષણાંકનું મૂલ્ય કેટલું હશે? (ગુરુત્વાકર્ષણને કારણે પ્રવેગ $g =10 \;ms ^{-2}$ લો)
JEE MAIN 2023, Medium
Download our app for free and get started
d
\(a=-\mu g\)
\(a=-\mu g\)
\(\because v=u+a t\)
\(0=20+(-\mu \times 10) \times 5\)
\(50 \mu=20\)
\(\mu=\frac{2}{5}=0.4\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10\,kg$ દળનો પદાર્થ $20\,m/s$ ના પ્રારંભિક વેગથી ગતિ કરે છે. પદાર્થ અને જમીન વચ્ચેના ઘર્ષણને કારણે પદાર્થ $5\,s$ પછી સ્થિર થાય છે. તો ઘર્ષણાંકનું મૂલ્ય કેટલું હશે? (ગુરુત્વાકર્ષણને કારણે પ્રવેગ $g =10 \;ms ^{-2}$ લો)View Solution
- 2$'m '$ દળના એક પદાર્થ ને સ્પ્રિંગના એક છેડે બાંધીને સમક્ષિતિજ સમતલમાં અચળ કોણીય વેગથી ચક્રાકારે ફેરવવામાં આવે છે. સ્પ્રિંગમાં ખેંચાણ $1\, cm$ છે. જો કોણીય વેગ બમણો કરવામાં આવે તો સ્પ્રિંગમાં ખેંચાણ $5\, cm$ થાય છે. તો સ્પ્રિંગની મૂળ લંબાઈ ........ $cm$ હશે.View Solution
- 3$5 \,kg$ દળના બ્લોક પર $4\, kg$ દળનું બાળક છે બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $0.5$ છે. બાળક દોરડા પર કેટલું મહતમ બળ ($N$ માં) લગાવી શકે કે જેથી બ્લોક ખસે નહીં? [$g=10 \,ms ^{-2}$ ]View Solution
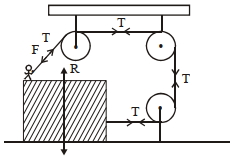
- 4$R_{1}$ અને $R_{2}$ અંદરની અને બહારની ત્રિજ્યા ધરાવતી વલયાકાર રિંગ સરક્યા વગર અચળ કોણીય ઝડપથી ફરે છે. રિંગના અંદરના અને બહારના ભાગો પર સ્થિત બે કણો દ્વારા અનુભવાતા બળોનો ગુણોત્તર, $\frac{F_{1}}{F_{2}}$ કેટલો થાય?View Solution
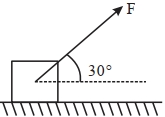
- 5$50\, kg$ નો બ્લોક રફ સપાટી પર પડેલ છે.બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $0.6$ છે.શિરોલંબ સાથે $30^°$ ખૂણે ...... $N$ લઘુત્તમ બળ લગાવવું જોઈએ કે જેથી બ્લોક માત્ર ગતિ કરવાનું શરૂ કરે.View Solution
- 6$1\, kg$ દળનો બ્લોક $\frac{1}{\sqrt{3}}$ સ્થિત ઘર્ષણાંક ધરાવતી સપાટી પર છે. બ્લોક પર $F\, N$ જેટલું લઘુતમ બળ લગાવતા તે ખસે છે. તો તો $F$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશે? [$g =10 \,ms ^{-2}$ ]View Solution
- 7$800 \mathrm{~kg}$ ની એક કાર $300 \mathrm{~m}$ ની ત્રિજ્યાં અને $30^{\circ}$ ના કોણવાળા ઢોળાવ વાળા રોડ ઉપર વળાંક લે છે. જો સ્થિતિ ઘર્ષણાંક $0.2$ હોય તો સુરક્ષિત રીતે ગાડી આ વળાંક લઈ શકે તે માટે મહત્તમ ઝડપ . . . . .હશે. $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2, \sqrt{3}=1.73\right)$ લો.View Solution
- 8આકૃતિમાં દર્શાવ્યા અનુસાર, સમક્ષિતિજ સપાટી ઉપર રહેલ $10\,kg$ ના દળને સમક્ષિતિજ સાથે $30^{\circ}$ ના કોણે $F$ બળથી ખેંચવામાં આવે છે.$\mu_{ s }=0.25$ માટે,બળ $F$ ના $........\,N$ મહતમ મૂલ્ય સુધી બ્લોક સ્થિર રહેશે.[$g=10\,ms^{-2}$ આપેલ છે.]View Solution
- 9$30^{\circ}$ ખૂણે રહેલ ઢાળ પર એક બ્લોક ઉપર તરફ $v_{0}$ જેટલા શરૂઆતના વેગથી ગતિ કરે છે. તે પોતાના મૂળ સ્થાને ફરીથી $\frac{v_{0}}{2}$ જેટલા વેગથી પાછો આવે છે. બ્લોક અને ઢાળ વચ્ચેના ગતિક ઘર્ષણાંકનું મૂલ્ય લગભગ $\frac{ I }{1000}$ હોય તો $I$ નું પૂર્ણાંકમાં મૂલ્ય લગભગ કેટલું હશે?View Solution
- 10એક પદાર્થ સંપૂર્ણ લીસા સમાન $45^{\circ}$ પર રહેલા ઢાળવાળા સમતલ પરથી સરકવા માટેના સમયના $\mathrm{n}$ ગણો સમય ખરબચડા $45^{\circ}$ પર રહેલા ઢાળવાળા સમતલ પર લાગે છે. પ્રદાથ અને ઢાળવાળા સમતલની સપાટી વચ્ચેનો ગતિક ઘર્ષણાંક. . . . . . . .છે.View Solution