$12.5\, eV$ ઉર્જા ધરાવતું ઇલેક્ટ્રોનપૂંજ રૂમ તાપમાને રહેલ હાઇડ્રોજન વાયુ પર પાડવામાં આવે છે. તો તે કેવી વર્ણપટ્ટ રેખાનું ઉત્સર્જન કરશે?
JEE MAIN 2013, Diffcult
a
\(\mathrm{E}=\frac{\mathrm{hc}}{\lambda} \Rightarrow \lambda=\frac{\mathrm{hc}}{\mathrm{E}}=\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{12.5 \times 1.6 \times 10^{-19}}\)
\(\mathrm{E}=\frac{\mathrm{hc}}{\lambda} \Rightarrow \lambda=\frac{\mathrm{hc}}{\mathrm{E}}=\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{12.5 \times 1.6 \times 10^{-19}}\)
\(=993 \mathrm{A}^{\circ}\)
\(\frac{1}{\lambda}=\mathrm{R}\left(\frac{1}{\mathrm{n}_{1}^{2}}-\frac{1}{\mathrm{n}_{2}^{2}}\right)\)
(where Rydberg constant, \(\mathrm{R}=1.097 \times 10^{7}\) )
\(\frac{1}{993 \times 10^{-10}}=1.097 \times 10^{7}\left(\frac{1}{1^{2}}-\frac{1}{n_{2}^{2}}\right)\)
Solving we get \(n_{2}=3\)
Spectral lines
Total number of spectral lines \(=3\)
Two lines in Lyman series for \(n_{1}=1, n_{2}=2\) and \(\mathrm{n}_{1}=1, \mathrm{n}_{2}=3\) and one in Balmer series for \(n_{1}=2, n_{2}=3\)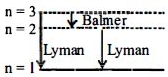
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\frac{1}{2} mv ^{2}$ જેટલી ઊર્જા ધરાવતાં આલ્ફા કણને $Ze$ જેટલો વિદ્યુતભાર ધરાવતા ભારે ન્યુક્લિયર પર આપાત કરવામાં આવે છે. કણનું સૌથી નજીકનાં સ્થાનનું અંતર (distance of closest approach) કોના સમપ્રમાણમાં હોય?View Solution
- 2હાઇડ્રોજન પરમાણુનો ઇલેક્ટ્રોન ઉત્તેજિત અવસ્થા $(n=3)$ માંથી ધરા અવસ્થા $(n=1)$ માં સંક્રાતિ પામે છે અને પરિણામે ઉત્સર્જીત ફોટોન્સને એક ફોટોસંવેદી પદાર્થ પર આપાત કરવામાં આવે છે. જો આ પદાર્થનું વર્ક ફંકશન $5.1\;eV$ છે, તો સ્ટોપિંગ પોટેન્શિયલનું મૂલ્ય ($V$ માં) આશરે કેટલું હશે? ($n$ મી કક્ષાના ઇલેક્ટ્રોનની ઉર્જા $E_n =\frac{-13.6}{n^2}\;eV$)View Solution
- 3હાઇડ્રોજનમાં પાશ્વન શ્રેણીની પ્રથમ તરંગલંબાઇ $18,800 \,\mathring A $ છે, તો પાશ્વન શ્રેણીની લધુત્તમ તરંગલંબાઇ કેટલા .......$ \,\mathring A $ મળે?View Solution
- 4હાઇડ્રોજનની $ n^{th} $ મી કક્ષામાં રહેલા ઇલેકટ્રોનની ઊર્જા $ {E_n} = - \frac{{13.6}}{{{n^2}}}eV $ છે,તો પ્રથમ કક્ષામાંથી બીજી કક્ષામાં ઇલેકટ્રોનને લઇ જવા માટે કેટલા .....$eV$ ઊર્જાની જરૂર પડે?View Solution
- 5જ્યારે ઈલેક્ટ્રોન $n=2$ થી $n = 1$ કક્ષામાં સંક્રાંતિ કરે ત્યારે હાઈડ્રોજન પરમાણું દ્વારા ઉત્સર્જાયેલા ફોટોનની તરંગલંબાઈ ...... $nm$ હશે.View Solution
- 6View Solutionહાઈડ્રોજન પરમાણુની પ્રથમ અને દ્વિતીય કક્ષામાં ઈલેક્ટ્રોનની ગતિના કારણે મળતાં સમતુલ્ય વિદ્યુત ભારનો ગુણોત્તર કેટલો થશે?
- 7View Solutionપરમાણુનો રાસાયણિક સ્વભાવ .......પર આધાર રાખે છે.
- 8હાઇડ્રોજન જેવા પરમાણુનો પરમાણુક્રમાંક $Z$ છે,તે $2n$ મુખ્ય કવોન્ટમઆંક ધરાવતી કક્ષામાં છે,તે મહત્તમ $204\, eV$ ઊર્જા ધરાવતો ફોટોનનું ઉત્સર્જન કરે છે, તે $n$ મુખ્ય કવોન્ટમઆંક ધરાવતી કક્ષામાં સંક્રાતિ કરે,ત્યારે $40.8 \,eV$ ઊર્જા ધરાવતો ફોટોનનું ઉત્સર્જન કરે છે, તો $n=$ ______View Solution
- 9View Solutionબોહરના પરમાણુ મોડેલ મુજબ, હાઇડ્રોજન પરમાણુમાં કઈ ઊર્જા ધરાવતા ફોટોનનું ઉત્સર્જન શક્ય નથી?
- 10$m$ દળનો એક નાનો કણ એવી રીતે ગતિ કરે છે કે તેની સ્થિતિઊર્જા $U=\frac{1}{2} m \omega^2 r ^2$ જ્યાં $\omega$ અચળાંક છે અને $r$ એ કણનું ઉગમબિંદુથી અંતર છે. બોહરના વેગમાન અને વર્તુળાકાર ભ્રમણકક્ષાનું ક્વોન્ટમીકરણને ધારતા, $n$ મી કક્ષાની ત્રિજ્યા કોના સમપ્રમાણમાં થશે?View Solution
