$1\,m$ લંબાઈના ધાતુના સળિયાને તેના એક છેડેથી એક સમતલમાં ફેરવવામાં આવે છે, એ સમતલ $2.5 \times 10^{-3}\; wb / m ^2$ ના ઈન્ડકટન્સથી લંબ છે. તે $1800\; revolution/ \min$ કરે. બંને છેડા વચ્ચે ઉદ્ભવેલું $induced\,emf..............\,V$
Medium
Download our app for free and get started
c
(c)
(c)
Given \(: \ell=1\,m , B =5 \times 10^{-3}\,Wb / m ^2\)
\(f =\frac{1800}{60}=30 \text { rotations } / sec\)
in one rotation, the moving rod of the metal races a circle of radius \(r=\ell\)
\(\therefore\) Area swept in one rotation \(=\pi r ^2\)
\(\frac{ d \phi}{ dt }=\frac{ d }{ dt }( BA )= B \cdot \frac{ dA }{ dt }=\frac{ B \pi r ^2}{ T }\)
\(= B f \pi r ^2=\left(5 \times 10^{-3}\right) \times 3.14 \times 30 \times 1=0.471 \,V\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionકોઇલની લંબાઈ અચળ રાખીને તેના આંટાની સંખ્યાને બમણી કરવામાં આવે, તો તેનું આત્મપ્રેરકત્વ કેટલું થાય?
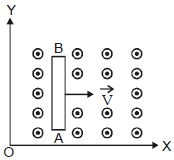
- 2સળિયા $X-$ અક્ષને સમાંતર અમુક વેગથી ગતિ કરે છે,તો $A$ છેડો ....View Solution
- 3$N$ આંટા ધરાવતી બે કોઇલ વચ્ચે અનોન્ય પ્રેરકત્વ $M$ છે.એક કોઇલમાં $t$ સમયમાં પ્રવાહ $I$ થી શૂન્ય કરવામાં આવે તો બીજી કોઇલમાં દરેક આંટા દીઠ ઉદભવતું $e.m.f. = .......$View Solution
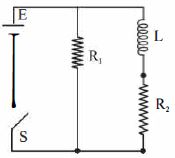
- 4એક $L =400 \;mH$ નો ઈન્ડકટર, $R _{1}=2 \;\Omega$ નો અવરોધ, અને $R _{2}=2 \;\Omega$ નો બીજો અવરોધ એ $12 \;V$ ના $emf$ વાળી બેટરી સાથે જોડેલા છે. બેટરીનો આંતરિક અવરોધ અવગણ્ય છે. $t=0$ સમયે સ્વીચ $s$ બંધ છે. $L$ આગળ વિદ્યુતસ્થિતિમાનમાં ધટાડો કેટલો થશે?View Solution
- 5આદર્શ કેપેસીટરનો કેપેસીટન્સ $0.2\, \mu F$ છે જેને $10\,V$ ના વિદ્યુતસ્થિતિમાનના તફાવતથી ચાર્જ કરવામાં આવે છે અને પછી તેમાથી મુક્ત કરવામાં આવે છે. પછી તેને $0.5\,mH$ આત્મપ્રેરકત્વ ધરાવતા આદર્શ ઇન્ડક્ટર સાથે જોડવામાં આવે છે. જ્યારે કેપેસીટર વચ્ચે વિદ્યુતસ્થિતિમાનનો તફાવત $5\,V$ હોય ત્યારે તેમાથી કેટલો પ્રવાહ ($A$ માં) વહેતો હશે?View Solution
- 6$80 cm^2 $ ક્ષેત્રફળ અને $50$ આંટા ધરાવતી તકતી $0.05Tesla$ ના ચુંબકીયક્ષેત્રમાં $2000 $ પરિભ્રમણ$/min$ થી ફરે છે,તો કેટલું $emf$ ઉત્પન્ન થાય?View Solution
- 7View Solutionઆદર્શ સ્ટેપ ડાઉન ટ્રાન્સફોર્મરમાં શેનું મૂલ્ય વધે છે?
- 8$10^{-2}\, T$ ઘરાવતા ચુંબકીય ક્ષેત્રના વિસ્તારમાં $30\,cm$ ત્રિજયા અને $ {\pi ^2} \;\Omega$ અવરોઘ ઘરાવતું વર્તુળાકાર ગૂંચળું મૂકેલ છે. આ ગૂંચળું ચુંબકીયક્ષેત્રને લંબ દિશામાં અને જે કોઇલનો વ્યાસ બનાવે છે. જો તે$200\, rpm$ ની ઝડપે ભ્રમણ કરે, તો ગૂંચળામાં ઉદ્ભવતા $AC$ પ્રેરિત પ્રવાહનું મૂલ્ય ($mA$ માં) કેટલું હશે?View Solution
- 9ગૂંચળાંમાંથી લંબરૂપે પસાર થતું ચુંબકીય ફ્લક્સ $\phi=\left(5 t^{3}+4 t^{2}+2 t-5\right)$ વેબર અનુસાર બદલાય છે. જે ગૂંચળાનો અવરોધ $5$ ઓહમ હોય તો ગૂંચળામાં $t=2 \,s$ એ પ્રેરિત પ્રવાહ $....\,A$ ગણો.View Solution
- 10એક ઇન્ડક્ટરનું ગુચળું $64\, {J}$ જેટલી ચુંબકીય ઉર્જાનો સંગ્રહ કરે છે અને જ્યારે તેમાંથી $8\, {A}$ નો પ્રવાહ પસાર કરવામાં આવે ત્યારે તે $640\, {W}$ ના દરથી ઉર્જા ગુમાવે છે. જો આ ગુંચળાને આદર્શ બેટરી સાથે જોડવામાં આવે તો આ પરિપથનો સમય અચળાંક ($sec$ માં) શોધો.View Solution