Impulse \(\mathrm{J}=0.2 \mathrm{~N}-\mathrm{S}\)
\(\mathrm{J}=\int \mathrm{Fdt}=0.2 \mathrm{~N}-\mathrm{s}\)
Angular impuls ( \(\overrightarrow{\mathrm{M}})\)
\(\overrightarrow{\mathrm{M}}_{\mathrm{c}}=\int \tau \mathrm{dt}\)
\(=\int \mathrm{F} \frac{\mathrm{L}}{2} \mathrm{dt}\)
\(=\frac{\mathrm{L}}{2} \int \mathrm{Fdt}=\frac{\mathrm{L}}{2} \times \mathrm{J}v\)
\(=\frac{0.3}{2} \times 0.2\)
\(=0.03\)
\(I_{c m}=\frac{\mathrm{LL}^2}{12}=\frac{2 \times(0.3)^2}{12}=\frac{0.09}{6}\)
\(\mathrm{M}=\mathrm{I}_{\mathrm{cm}}\left(\omega_{\mathrm{f}}-\omega_{\mathrm{i}}\right)\)
\(0.03=\frac{0.09}{6}\left(\omega_{\mathrm{f}}\right)\)
\(\omega_{\mathrm{f}}=2 \mathrm{rad} / \mathrm{s}\)
\(\theta=\omega \mathrm{t}\)
\(\mathrm{t}=\frac{\theta}{\omega}=\frac{\pi}{2 \times 2}=\frac{\pi}{4} \mathrm{sec} .\)
\(\mathrm{X}=4\)
Download our appand get started for free
Similar Questions
- 1$M$ દળ ધરાવતા અને $R$ ત્રિજયા ધરાવતા ઘન ગોળામાંથી મહત્તમ કદ ધરાવતો એક સમઘન કાપવામાં આવે છે,તેના કેન્દ્રમાંથી પસાર થતી અને તેની કોઇ એક બાજુને લંબ એવી અક્ષને અનુલક્ષીને ચાકમાત્રા ________ થશે.View Solution
- 2View Solutionનૃત્યકાર ચાકગતિ કરતા પ્લેટફોર્મ પર હાથમાં બે ગોળા લઈને ઊભો છે. જો તે ગોળા જમીન પર પડી જાય તો નૃત્યકારની...
- 3View Solutionઆકૃતિમાં કઇ અક્ષ પર કોણીય પ્રવેગ વધુ થશે અને બળ ત્રિકોણ ફ્રેમના મધ્યબિંદુ પર લાગે છે.
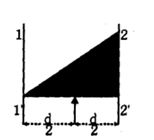
- 4એક તક્તી સ્થિર સ્થિતિથી તેની અક્ષને અનુલક્ષીને પરિભ્રમણ કરી રહી છે, તે $4 \,s$ માં $100 \,rev / s$ ની કોણીય ઝડપ પ્રાપ્ત કરે છે. આ $4 \,s$ દરમિયાન પરિભ્રમણ થયેલો ખૂણો (રેડીયનમાં) ......... $\pi$ થાય?View Solution
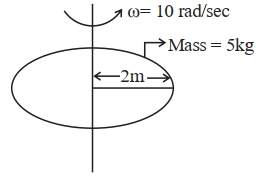
- 5એક $5 \mathrm{~kg}$ દળ, $2 \mathrm{~m}$ ત્રિજ્યા અને તેના પરિભ્રમણ સમતલને લંબ અક્ષને અનુરુપ કોણીય વેગ $10 \mathrm{rad} / \mathrm{sec}$ ધરાવતી એક તક્તિ ધ્યાનમાં લો. આ જ અક્ષની દિશામાં બીજી એક સમાન તક્તિને હળવેકથી ભ્રમણ કરતી તક્તિ ઉપર મૂકવામાં આવે છે. બંને તક્તિઓ સરક્યા સિવાય એકબીજા સાથે પરિભ્રમણ કરે તે માટે વિખેરીત થતી ઊર્જા_____________$j$ છે .View Solution
- 6એક નક્કર ગોળો $A$ અને બીજો પોલો ગોળો $B$ સમાન દળ અને સમાન બાહ્ય ત્રિજ્યા ધરાવે છે. તેમના વ્યાસને અનુલક્ષીને જડત્વની ચાકમાત્રા અનુક્રમે $I_{A}$ અને $I_{B}$ ....View Solution
જ્યાં $d_{A}$ અને $d_{B}$ તેમની ઘનતા છે
- 7View Solutionપૃથ્વીની અંદરથી વિવિધ પ્રકારના ખનીજોને ખોદવામાં આવે છે, અને બહુમાળીય ઈમારતો બાંધવામાં આવે છે. આ પ્રવૃતિને કારણો સૈદ્ધાંતિક રીતે,
- 8એક વર્તૂળાકાર તકતી $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. જો તકતી પર બાળક બેસે, તો શેનું સંરક્ષણ થશે ?View Solution
- 9$50\; kg$ દ્રવ્યમાન તથા $0.5\;m$ ત્રિજયાનો એક ઘન નળાકાર, તેની સમક્ષિતિજ અક્ષને અનુલક્ષીને મુકત રીતે પરિભ્રમણ કરી શકે છે. તેના પર વજનરહિત દોરી એવી રીતે વીંટાળેલી છે કે જેનો એક છેડો આ નળાકાર સાથે બાંધેલો છે અને બીજો છેડો મુક્ત રીતે લટકાવેલો છે. દોરી પર કેટલું તણાવબળ ($N$ માં) લગાડવામાં આવે કે જેથી કોણીય પ્રવેગ $2$ પરિભ્રમણ/સેકન્ડ$^2$ થાય?View Solution
- 10View Solutionસમાન દળ અને ત્રિજ્યાનો એક નક્કર નળાકાર અને એક નક્કર ગોળો એક ખરબચડા ઢોળાવ વાળા સમતલ ઉપર સરક્યાં વિના ગબડે છે. ઘર્ષણ નું બળ કેટલું થાય?
