\(v _{ s }=\sqrt{\frac{\gamma RT }{ M }}\)
\(v _{ mms }=\sqrt{\frac{3 RT }{ M }}\)
\(\frac{ v _{ s }}{ v _{ rms }}=\sqrt{\frac{\gamma}{3}}=\frac{1}{\sqrt{2}} \Rightarrow \frac{\gamma}{3}=\frac{1}{2} \Rightarrow \gamma=\frac{3}{2}\)
\(\gamma=1+\frac{2}{ f _{\operatorname{mix}}}\)
\(f _{\operatorname{mix}}=\frac{2 \times 3+ n \times 5}{ n +2}=\frac{6+ n \times 5}{( n +2)}\)
\(\gamma=1+\frac{2( n +2)}{6+ n \times 5}=\frac{6+5 n +2 n +4}{6+5 n }\)
\(\gamma=\frac{7 n +10}{6+5 n }=\frac{3}{2}\)
\(14 n +20=18+15 n\)
\(n =2\)
Download our appand get started for free
Similar Questions
- 1એક વાયુ મિશ્રણમાં $2\, mol $ ઓકિસજન અને $4 \,mol$ આર્ગોન વાયુ $T$ તાપમાને ભરેલા છે. જો કંપનગતિને અવગણવામાં આવે, તો તંત્રની કુલ આંતરિક ઊર્જા કેટલી થશે?View Solution
- 2$\mathrm{CH}_4$ અણુ માટે રૅખીયગતિ માટે મુક્તતાનાં અંશી $\left(f_t\right)$ અને યાકગતિ માટે મુક્તતાનાં અંશો $\left(f_r\right)$,. . . . . . . . .છે.View Solution
- 3આદર્શવાયુ$(\gamma = 1.5) $ ને સમોષ્મી વિસ્તરણ દ્રારા કેટલાં ગણુ કદ કરવાથી $rms$ ઝડપ અડધી થાય.View Solution
- 4$1\, kg$ દ્વિ આણ્વિય વાયુ $8 \times 10^4$ $N/m^{2}$ દબાણે છે. વાયુની ઘનતા $4 kg/m^3$ છે. વાયુની ઉષ્મિય ગતિના કારણે ઊર્જા શું થશે?View Solution
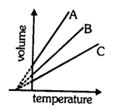
- 5$m$ દળના આદર્શ વાયુનું અચણ દબાણ $P$ એ કદનું વિસ્તરણ આલેખમાં સુરેખ રેખા $B$ દ્વારા દર્શાવેલું છે. ત્યારે તે આદર્શ વાયુના $2m$ દળનું $2P$ દબાણે કોઈ સુરેખ રેખા દર્શાવે છે?View Solution
- 6પાત્રમાં રહેલો ગેસનું દબાણ $ {P_0} $ છે.હવે અણુનું દળ અડધું અને ઝડપ બમણી કરતાં નવું દબાણ કેટલુ થાય?View Solution
- 7અચળ દબાણ અને અચળ કદે વિશિષ્ટ ઉષ્માઓ અનુક્રમે $c_p$ અને $c_v$ છે.એવું જોવામાં આવ્યું કે હાઇડ્રોજન વાયુ માટે $c_P- c_V= a$ , નાઇટ્રોજન વાયુ માટે $c_P-c_V=b$ $a$ અને $b$ વચ્ચેનો સંબંઘ છે:View Solution
- 8મુક્તતા અંશો માટે ક્યું વિદ્યાન સાયું છે ?View Solution
$(A)$ $n$ મુક્તતાનાં અંશો ધરાવતા એક અણુ પાસે $n ^2$ જેટલા ઊર્જા સંગ્રહ કરવાના જુદા-જુદા રસ્તાઓ હશે.
$(B)$ દરેક મુક્તતા અંશ એ પ્રતિ મોલ સરેરાશ ઊર્જાના $\frac{1}{2}RT$ સાથે સંકળાયેલા હશે.
$(C)$ એક પરમાણ્વીય વાયુ અણુ પાસે એક ભ્રમણ ગતિકીય મુક્તતા અંશ જ્યારે દ્વિપરમાણ્વીય પાસે બે ભ્રમણાગતિકીય મુક્તતા અંશો હશે.
$(D)$ $CH _4$ પાસે કુલ $6$ મુક્તતા અંશો હશે.
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 9દઢ ના હોય તેવા $10$ દ્વિ-પરમાણ્વીક અણુઓની $T$ તાપમાને ઉીર્મ. . . . થશે.View Solution
- 10જો $V_H, V_N$ અને $V_O$ એ આપેલા તાપમાને અનુક્રમે હાઈડ્રોજન, નાઈટ્રોજન અને ઓક્સિજન પરમાણુનો $rms$ વેગ દર્શાવે ત્યારે......View Solution
