$20\, cm$ અને $10\, cm$ ત્રિજ્યાના બહે ધાતુના દરેક પોલા ગોળાઓ પર $150\ \mu C$ નો વિદ્યુતભાર છે. તો તેમને તાર વડે જોડતાં સામાન્ય વિદ્યુતસ્થિતિમાન ...... $V$ છે.
Medium
Download our app for free and get started
a
અહી બંને પોલા ગોળાઓનું જોડાણ સમાંતર ગણાય .
અહી બંને પોલા ગોળાઓનું જોડાણ સમાંતર ગણાય .
તેથી તેમનું પરિણામી કેપેસીટન્સ \({C_1} + {C_2} = \frac{{{R_1} + {R_2}}}{k}\)
જોડાણ નું સામાન્ય સ્થિતિમાન \(V = \frac{{{q_1} + {q_2}}}{{{C_1} + {C_2}}}\)
\(V = \frac{{150 \times {{10}^{ - 6}} + 150 \times {{10}^{ - 6}}}}{{\frac{{{R_1} + {R_2}}}{k}}}\,\,\therefore \,V = \frac{{3 \times {{10}^{ - 14}} \times k}}{{{R_1} + {R_2}}}\,\,\,\)
\(\therefore \,V = \frac{{3 \times {{10}^{ - 14}} \times 9 \times {{10}^9}}}{{3 \times {{10}^{ - 1}}}}\,\,\therefore \,V = 9 \times {10^6}\ V\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચે બે વિધાનો આપેલાં છે. એકને કથન $A$ અને બીજાને કારણા $R$ વડે દર્શાવેલ છે.View Solution
કथન $A: 4 \times 10^{-6} \mathrm{C}$ $m$ના મૂલ્યની દ્રી-ધ્રુવી ચાકમાત્રા $\vec{P}$. ધરાવતી દ્રી-ધ્રુવીના કેન્દ્રથી $2 \mathrm{~m}$ અંતરે $(r)$ રહેલ કોઈ અક્ષીય બિંદુ આગળ સ્થિતિમાન $(\mathrm{V}) \pm 9 \times 10^3 \mathrm{~V}$ છે.
$\left[\frac{1}{4 \pi \epsilon_0}=9 \times 10^9 \text { SI એકમ }\right]$
કારણ $R: V= \pm \frac{2 P}{4 \pi \epsilon_0 r^2}$, જ્યાં $r$ એ કોઈ અક્ષીય બિંદુનું
ત્રિજ્યાવર્તી દિશામાં અંતર છે કે જે દ્વિ-ધ્રુવીનાં કેન્દ્રથી $2 \mathrm{~m}$ અંતરે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં નીચે આપેલા વિક્લ્પોમાંથી સાચો ઉત્તર ૫સંદ કરો.
- 2$5\,mm$ બે પ્લેટ વચ્ચેનું અંતર ધરાવતા સમાંતર પ્લેટ કેપેસીટરનું કેપેસીટન્સ $3\,F$ હોય તો પ્લેટનું ક્ષેત્રફળ મેળવોView Solution
- 3$6\ \mu F$ ના કેપેસીટરને $10\, volts$ થી $20 \,volts$ વિદ્યુતભારીત કરેલ છે તો ઉર્જામાં થતો વધારો.....View Solution
- 4View Solutionધ્રુવીય અણુઓ .... અણુઓ છે.
- 5$3\,\mu \,F,\,10\,\mu \,F\,$ અને $15\,\mu \,F\,$ ના કેપેસીટરને $100\,V$ ની બેટરી સાથે શ્રેણીમાં જોડેલા હોય તો $15\,\mu \,F\,$ પર રહેલો વિધુતભાર .......$\mu C$ થાયView Solution
- 6કેપેસિટરને $100\, V$ ચાર્જ કરવામાં આવે છે.તેમાં $2\,mm$ ડાઇઇલેકિટ્રક પ્લેટ નાખતાં પહેલા જેટલો વોલ્ટેજ કરવા માટે બે પ્લેટ વચ્ચેનું અંતર $1.6\,mm$ વધારવું પડે છે.તો ડાઇઇલેકિટ્રકનો ડાઇઇલેકિટ્રક અચળાંક કેટલો હશે?View Solution
- 7વિદ્યુત દ્વિધ્રુવી થી ' $r$ ' અંતરે સ્થિત વિદ્યુત સ્થિતિમાન________મુજબ બદલાય છે.View Solution
- 8$d$ જેટલું પ્લેટોનું અંતર ધરાવતા કેપેસીટરને $V$ સ્થિતિમાટે રાખેલ છે. બેટરીથી છુટો કરી દીધા બાદ તેનામાં $\frac{d}{2}$ જેટલી જાડાઈનો એવો ડાઈઇલેક્ટ્રીક દાખલ કરાય છે કે જેને ડાઈઇલેકટ્ટીક અચળાંક $2$ છે. હવે તેનાં બે છેડાઓ વચ્ચે વિદ્યુત સ્થિતિમાનનો તફાવત કેટલો રહેશે ?View Solution
- 9એક $C$ કેપેસીટન્સ ધરાવતા કેપેસીટરને $V _{0}$ જેટલા વૉલ્ટેજ ધરાવતા સ્ત્રોત સાથે જોડીને ચાર્જ કરેલ છે, પછી તેને સ્ત્રોતથી અલગ કરી બીજા $\frac{ C }{2} $ કેપેસીટન્સ ધરાવતા કેપેસીટર સાથે સમાંતરમાં જોડવામાં આવે છે. બંને કેપેસીટર પર વિજભારના વિતરણની પ્રક્રિયા દરમિયાન થતો ઉર્જાનો વ્યય $.........\;CV _{0}^{2}$ જેટલો હશે?View Solution
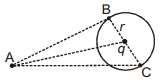
- 10$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
