$20 \,{cm}$ ત્રિજ્યા અને $10\, {kg}$ દળ ધરાવતી ઘન તકતી તેના વર્તુળાકાર સમતલને લંબ અને તેના દ્રવ્યમાનકેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $600\, {rpm}$ ના કોણીય વેગથી ફરે છે. તકતીને $10\, {s}$ માં સ્થિ કરવા માટે જરૂરી ટોર્ક ($......\, \pi \times \,10^{-1}\, {Nm}$ માં) કેટલું હશે?
JEE MAIN 2021, Medium
Download our app for free and get started
d
\(\tau=\frac{\Delta L}{\Delta t}=\frac{I\left(\omega_{f}-\omega_{i}\right)}{\Delta t}\)
\(\tau=\frac{\Delta L}{\Delta t}=\frac{I\left(\omega_{f}-\omega_{i}\right)}{\Delta t}\)
\(\tau=\frac{\frac{m R^{2}}{2} \times[0-\omega]}{\Delta t}\)
\(=\frac{10 \times\left(20 \times 10^{-2}\right)^{2}}{2} \times \frac{600 \times \pi}{30 \times 10}\)
\(=0.4 \pi=4 \pi \times 10^{-2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
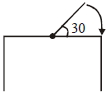
- 1$1\; \mathrm{m}$ લાંબા સળિયાનો એક છેડો સમક્ષિતિજ ટેબલ પર જડેલો છે.જ્યારે તે સમક્ષિતિજ સાથે $30^{\circ}$ નો ખૂણો બનાવે ત્યારે તેણે મુક્ત કરવામાં આવે છે.તે જ્યારે ટેબલ સાથે અથડાય ત્યારે તેનો કોણીય વેગ $\sqrt{\mathrm{n}}\; \mathrm{s}^{-1}$ આપવામાં આવે છે જ્યાં $\mathrm{n}$ એ પૂર્ણાંક સંખ્યા હોય તો $n$ મૂલ્ય કેટલું હશે?View Solution
- 2$R$ અને $ nR$ ત્રિજ્યાની બે સમાન રિંગના કેન્દ્રમાંથી પસાર થતી અક્ષ પર જડત્વની ચાકમાત્રાનો ગુણોત્તર $1 : 8$ છે. તો $ n$ ની કિંમત શું થશે ?View Solution
- 3$l$ લંબાઈને ચોરસ $ABCD$ ના ખૂણાઓ પર ચાર બિંદુવત્ દળો (દરેક નું દળ $m$) મૂકવામાં આવે છે. તો $BD$ ને સમાંતર એવી $A$ માંથી પસાર થતી અક્ષને અનુલક્ષીને તંત્રની જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 4View Solutionકઈ અક્ષ પર રિંગની જડત્વની ચાકમાત્રા મહત્તમ થશે ?
- 5જેની દળ ધનતા $\rho{=\rho_0}\left(1-\frac{x^2}{L^2}\right) kg / m$ અને લંબાઈ $L$ (મીટરમાં) હોય તેવા એક પરિમાણીય સળિયાનું, એક છેડાથી દ્રવ્યમાન કેન્દ્ર $\frac{3 L}{\alpha}$ મીટર છે. $\alpha$ નું મૂલ્ય $........$ હશે.View Solution
- 6View Solutionકોઈ પદાર્થના જડત્વની ચાકમાત્રા શેના ઉપર આધાર રાખે છે?
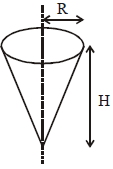
- 7આકૃતિમાં પોલો આઇસ્ક્રીમ કોન છે ,તેનું દળ $M,$ ઉપરની ત્રિજ્યા $R$ અને ઊંચાઈ $H$ છે,તો આપેલી અક્ષને અનુલક્ષીને જડત્વની ચાક્માત્રા ......View Solution
- 8$1\ kg$ નો એક પદાર્થ $2\ ms^{-1}$ જેટલા રેખીય વેગથ ધન $X -$ અક્ષને સમાંતર ગતિ કરી રહ્યો છે. આ ગતિ દરમિયાન ઉગમબિંદુથી તેનું લઘુતમ અંતર $ 12\ cm $ થાય છે, તો આ પદાર્થનું ઉગમબિંદુને અનુલક્ષીને કોણીય વેગમાન ....... $Js$View Solution
- 9$M$ દળ ધરાવતા તારને $ R $ ત્રિજ્યાવાળા વર્તૂળાકારે વાળવામાં આવે છે, તો આ વર્તૂળના વ્યાસને અનુલક્ષીને જડત્વની ચાકમાત્રા .......View Solution
- 10યામતંત્રના ઉગમબિંદુ પર $-P \hat{k}$ બળ લાગે છે. બિંદુુ $(2,-3)$ ને અનુલક્ષી ટોર્ક $P(a \hat{i}+b \hat{j})$ છે. ગુણોતર $\frac{a}{b}$ નું મૂલ્ય $\frac{x}{2}$ છે. તો $x$ ની કિંમત ........ છે.View Solution