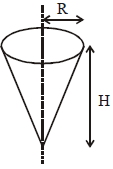
Area \(=\pi R \ell=\pi R \left(\sqrt{ H ^{2}+ R ^{2}}\right)\)
Area of element \(d A =2 \pi rd \ell==2 \pi r \frac{ dh }{\cos \theta}\)
mass of element \(dm =\frac{ M }{\pi R \sqrt{ H ^{2}+ R ^{2}}} \times \frac{2 \pi rdh }{\cos \theta}\)
\(dm =\frac{2 Mh \tan \theta dh }{ R \sqrt{ H ^{2}+ R ^{2}} \cos \theta} \quad\) (here \(\left. r = h \tan \theta\right)\)
\(I =\int( dm ) r ^{2}=\int \frac{ h ^{2} \tan ^{2} \theta}{\cos \theta}\left(\frac{2 m }{ R } \frac{ h \tan \theta}{\sqrt{ R ^{2}+ H ^{2}}}\right) dh\)
\(=\frac{2 M }{\cos \theta R } \frac{\tan ^{3} \theta}{\sqrt{ R ^{2}+ H ^{2}}}\)
\(\int_{0}^{ H } h ^{3} dh =\frac{ MR ^{2} H ^{4}}{2 RH ^{3} \sqrt{ R ^{2}+ H ^{2}} \cos \theta}\)
\(=\frac{ MR ^{2} H \sqrt{ R ^{2}+ H ^{2}}}{2 \sqrt{ R ^{2}+ H ^{2}} \times H }\)
\(=\frac{ MR ^{2}}{2}\)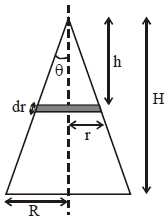
Download our appand get started for free
Similar Questions
- 1એક ધન ગોળો અને એક પોલો નળાકાર સમાન ટોળાવ ઉપર સમાન પ્રારંભિક ઝડ૫ $v$ થી સરકયા સિવાય ઉપર તરફ ગબડે છે. ગોળો અને નળાકાર પ્રારંભિક લેવલ (સ્થાન) થી અનુક્મે ઉપર $h_1$ અને $h_2$ જેટલી મહતમ ઉંચાઇઓએ પહોંચે છે. $h_1: h_2$ ગુણોત્તર $\frac{n}{10}$ છે. $\mathrm{n}$ નું મૂલ્ય. . . . . . . થશે.View Solution
- 2$m$ અને $M$ દળના બે પદાર્થ ને $L$ અંતરે મૂકેલા છે. તો $m$ દળ ના પદાર્થ પાસેથી દ્રવ્યમાનકેન્દ્રનું અંતર કેટલુ થાય$?$View Solution
- 3$R$ ત્રિજ્યા અને $9M$ દળની વર્તુળાકાર તકતીમાંથી સમકેન્દ્રિય રહેલ $\frac{R}{3}$ ત્રિજ્યા અને $M$ દળની નાની તકતીને દૂર કરવામાં આવે છે. બાકી રહેલી તકતીની તકતીના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 4જો એક ઘન ગોળો અને નળાકાર ની ત્રિજ્યા અને ઘનતા સમાન હોય તો તેની પોતાની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કોના માટે મહત્તમ હોય $(L=R )$ ?View Solution
- 5$m$ દળ અને $l$ લંબાઇ ધરાવતા સળિયાના મધ્યબિંદુ અને છેડાની મધ્યમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 6નીચે આપેલા પદાર્થોને એક ઢાળ પર નીચેથી ઉપર તરફ (સરક્યાં વગર) ભ્રમણ કરવવામાં આવે છેView Solution
$(i)$ $R$ ત્રિજ્યાની રિંગ
$(ii)$ $\frac {R}{2}$ ત્રિજ્યાનો ઘન નળાકાર અને
$(iii)$ $\frac {R}{4}$ ત્રિજ્યાનો ઘન ગોળો
જો ઢાળના તળિયે બધાના દ્રવ્યમાન કેન્દ્રનો વેગ સમાન હોય તો તેમના દ્વારા પ્રાપ્ત થતી મહત્તમ ઊંચાઈનો ગુણોત્તર કેટલો થાય?
- 7એક કારનું વજન $1800\; kg$ છે. તેની આગળ અને પાછળની એક્સેલ્સ (ધરીઓ) વચ્ચેનું અંતર $1.8\; m$ છે. તેનું ગુરુત્વકેન્દ્ર આગળની એક્સલથી $1.05\; m$ પાછળ છે. સમતલ જમીન દ્વારા આગળના દરેક પૈડા (વ્હીલ) પર લાગતું બળ શોધો.View Solution
- 8View Solutionએક વર્તુળાકાર તકતીને તેના સમતલમાંથી પસાર થતી સ્પર્શીય અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજયા અને સમાન ત્રિજ્યા ધરાવતી વર્તુળાકાર રિંગના સમતલમાં પસાર થતી સ્પર્શીય અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજયાનો ગુણોત્તર કેટલો થાય?
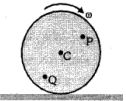
- 9તકતી સપાટી પર શુદ્ધ રોલિંગ કરે છે. કોઈ ક્ષણે $ P$ અને $ Q$ ના સ્થાન આકૃતિમાં દર્શાવેલા છે.$C $ એ તકતીનું કેન્દ્ર છે. જે ક્ષણે $ P$ અને $ Q$ કેન્દ્રથી સમાન અંતરે હોય ત્યારે તેના વેગ માટે નીચેનામાંથી કયું સાચું છે ?View Solution
- 10એક $8\,kg$ દળ ધરાવતા પદાર્થને $2\,kg$ દળ અને $1\,m$ લંબાઈ ધરાવતા એક નિયમિત સળિયા $CD$ ના એક છેડાથી લટકાવેલ છે, સળિયાનો બીજો છેડો આકૃતિમાં દર્શાવ્યા અનુસાર ઉર્ધ્વ (શિાોલંબ) દિવાલ સાથે ટકાવેલ છ. તે સળિયાને $A B$ તાર (કેબલ) વડે અવી રીતે ટેકવેલો છે કે જથી તંત્ર સંતુલનમાં રહે. કેબલમાં તણાવ $............\,N$ હશે.(ગુરુત્વીયપ્રવેગ $g=10\,m / s ^2$ )View Solution