\(\text { Here, } L=20\, \mathrm{mH}=20 \times 10^{-3}\, \mathrm{H}\)
\(C=50\, \mu \mathrm{F}=50 \times 10^{-6}\, \mathrm{F}\)
\(R=40\, \Omega, V=10\, \sin \,340\, t=V_{0} \sin \omega t\)
\(\omega=340 \,\mathrm{rad} \,\mathrm{s}^{-1}, V_{0}=10\, \mathrm{V}\)
\(X_{L}=\omega L=340 \times 20 \times 10^{-3}=6.8\, \Omega\)
\(X_{C}=\frac{1}{\omega C}=\frac{1}{340 \times 50 \times 10^{-6}}=\frac{10^{4}}{34 \times 5}=58.82 \,\Omega\)
\(Z=\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}=\sqrt{(40)^{2}+(58.82-6.8)^{2}}\)
\(=\sqrt{(40)^{2}+(52.02)^{2}}=65.62\, \Omega\)
The peak current in the circuit is
\(I_{0}=\frac{V_{0}}{Z}=\frac{10}{65.62} \,\mathrm{A}, \cos \phi=\frac{R}{Z}=\left(\frac{40}{65.62}\right)\)
Power loss in \(A.C.\) circuit,
\({=V_{\mathrm{rms}} I_{\mathrm{rms}} \cos \phi=\frac{1}{2} V_{0} I_{0} \cos \phi}\)
\({=\frac{1}{2} \times 10 \times \frac{10}{65.62} \times \frac{40}{65.62}=0.46 \,\mathrm{W}}\)
Download our appand get started for free
Similar Questions
- 1ફક્ત ઈન્ડકટર ધરાવતા પરિપથમાં પ્રવાહનું સમીકરણ $5 \sin \left(49 \pi t -30^{\circ}\right)$ છે. જે પ્રેરકત્વ $30 \,mH$ હોય, તો ઈન્ડકટરને સમાંતર વોલ્ટેજનું સમીકરણ .............. થશે. $\left\{\pi=\frac{22}{7}\right\}$ .View Solution
- 2$L,C$ અને $R$ ને $f$ આવૃત્તિવાળા $AC$ ઉદ્ગમ સાથે જોડતાં પ્રવાહ વોલ્ટેજ કરતાં કળામાં $45°$ આગળ છે,તો $C$ કેટલો થાય?View Solution
- 3નીચે બે વિધાનો આપવામાં આવ્યા છે:View Solution
વિધાન$-I:$ $ac$ પરિપથમાં કેપેસિટરનો પ્રવાહ તેના વોલ્ટેજ કરતાં આગળ હોય છે.
વિધાન$-II:$ માત્ર શુદ્ધ કેપેસીટન્સ ધરાવતા $a.c.$ પરિપથમાં, પ્રવાહ અને વોલ્ટેજ વચ્ચેનો કળા તફાવત $\pi$ હોય છે
ઉપરોક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય જવાબ પસંદ કરો.
- 4દોલનો કરતાં $L-C$ પરિપથમાં કેપેસિટર પર મહત્તમ વિદ્યુતભાર $Q$ છે. જ્યારે વિદ્યુતક્ષેત્ર અને ચુંબકીય ક્ષેત્ર વચ્ચે સમાન રીતે ઊર્જા સંગ્રહિત થાય ત્યારે કેપેસિટર પરનો વિદ્યુતભાર કેટલો હશે?View Solution
- 5$L-C-R$ પરિપથમાં $C = 10^{-11}\,Farad.$ $L = 10^{-5}\,Henry$ અને $R =100\,Ohm$ છે જ્યારે આ પરિપથને અચળ $E$ વૉલ્ટેજ ધરાવતા $D.C.$ સ્ત્રોત સાથે જોડવામાં આવે તો કેપેસીટર $10^{-9}\,C$ જેટલો વિજભાર પ્રાપ્ત કરે છે. આ $D.C.$ સ્ત્રોતને $sin$ વિધેય પર આધારિત વૉલ્ટેજ સ્ત્રોત સાથે જોડવામાં આવે છે જેનો મહત્તમ વૉલ્ટેજ $E_0$ એ $D.C.$ સ્ત્રોતના અચળ વૉલ્ટેજ $E$ જેટલો છે. અનુનાદ સમયે કેપેસીટર દ્વારા પ્રાપ્ત થતાં મહત્તમ વિજભારનું મૂલ્ય કેટલું હશે?View Solution
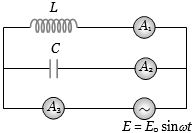
- 6આકૃતિમાં બતાવ્યા અનુસાર ઇન્ડક્ટર $ L $ અને કેપેસિટર $ C $ સર્કિટમાં જોડાયેલ છે. વીજ પુરવઠાની આવર્તન સર્કિટની રેઝોન્ટ આવર્તન સમાન છે. કયુ એમીટર ઝીરો એમ્પીયર વાંચશે?View Solution
- 7$0.7\,H$ ઇન્ડકટર અને $220\,\Omega$ અવરોધને $220\,V , 50\,Hz$ ના $a.c.$ ઉદગમ સાથે જોડવામાં આવે છે,તો પ્રવાહ એ વૉલ્ટેજમાં કેટલી કળામાં પાછળ અને પ્રવાહ શોધો.View Solution
- 8કોઈ સમયે $AC$ પરિપથનો $e.m.f\;(\varepsilon)$ અને પ્રવાહ $(i)$ અનુક્રમે $E=E_o sin(\omega t)$ અને $I=I_osin\left( {\omega t - \phi } \right)$ છે. $a.c.$ પરિપથનો એક ચક્ર દરમિયાન સરેરાશ પાવર કેટલો થાય?View Solution
- 9$LCR$ શ્રેણી પરિપથમાં ઇન્ડકટર,અવરોધ અને કેપેસિટરના વોલ્ટેજ $46,8$ અને $40 V$ છે,તો $A.C$. વોલ્ટેજ કેટલો થાય?View Solution
- 10સૂયિ-$I$ અને સૂયિ-$II$ મેળવોઃView Solution
નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરોઃ