\({T_2} = T\) (say), \(T = {25\,^o}C = 298\,K\),
\({E_a} = 104.4\,{\rm{kJ}}\,mo{l^{ - 1}} = 104.4 \times {10^3}\,{\rm{J}}\,mo{l^{ - 1}}\)
\({K_1} = 3 \times {10^{ - 4}},\,\,{K_2} = \)?,
\(\log \frac{{{K_2}}}{{{K_1}}} = \frac{{{E_a}}}{{2.303R}}\left[ {\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}} \right]\)
\(\log \frac{{{K_2}}}{{3 \times {{10}^{ - 4}}}} = \frac{{104.4 \times {{10}^3}{\rm{J}}\,\,mo{l^{ - 1}}}}{{2.303 \times (8.314\,\,{\rm{J}}\,\,{k^{ - 1}}\,\,mo{l^{ - 1}})}}\)
\(\left[ {\frac{1}{{298\,K}} - \frac{1}{T}} \right]\,\,{\rm{As}}\,\,{\rm{T}} \to \infty {\rm{,}}\frac{{\rm{1}}}{{\rm{T}}} \to 0\)
\(\therefore \,\,\log \frac{{{K_2}}}{{3 \times {{10}^{ - 4}}}} = \frac{{104.4 \times {{10}^3}\,\,{\rm{J}}\,\,mo{l^{ - 1}}}}{{2.303 \times 8.314 \times 298}}\)
\(\log \frac{{{K_2}}}{{3 \times {{10}^{ - 4}}}} = 18.297,\,\,\frac{{{K_2}}}{{3 \times {{10}^{ - 4}}}}\) \( = 1.98 \times {10^{18}}\) or
\({K_2} = (1.98 \times {10^{18}}) \times (3 \times {10^{ - 4}}) = 6 \times {10^{14}}\,{s^{ - 1}}\)
Download our appand get started for free
Similar Questions
- 1$A + B$ $\rightleftharpoons$ $AB$ જો પ્રક્રિયાના $A$ અને $B$ ની સાંદ્રતા બમણી હોય તો પ્રક્રિયાનો દર ....... થશે.View Solution
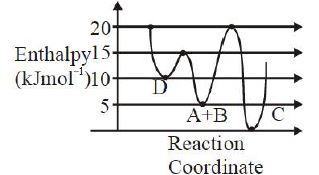
- 2$A$ અને $B$ વચ્ચેની નીચેની પ્રક્રિયાની એન્થાલ્પીનો આપેલ આલેખ ધ્યાનમાં લો. $A + B \to C + D$View Solution
ખોટું વિધાન ઓળખો.
- 3નીચે આપેલા પ્રકિયા ને ધ્યાન માં લો, વેગ અભિવ્યક્તિ કે જે નીચે આપેલ છે.View Solution
$\mathrm{A}+\mathrm{B} \rightarrow \mathrm{C}$
$\text { rate }=\mathrm{k}[\mathrm{A}]^{1 / 2}[\mathrm{~B}]^{1 / 2}$
$A$ અને $B$ એમ દરેક ની સાદ્રતા $1 M$ લઇ ને પ્રક્રિયા શરૂ કરવામાં આવે છે. જો વેગ અયળાંક ($k$) એ $4.6 \times 10^{-2} \mathrm{~s}^{-1}$, હોય તો $A$ ને $0.1 \mathrm{M}$ થવા માટે જરૂરી સમય .................. sec છે. (નજીક નો પૂર્ણાંક)
- 4View Solutionદ્વિતીય ક્રમની પ્રક્રિયા માટે વેગ-અચળાંકનો એકમ ......
- 5View Solutionવેગ અચળાંકનો એકમ કોના ઉપર આધાર રાખે છે ?
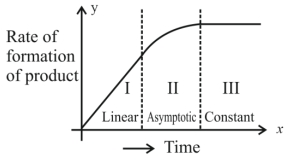
- 6એક નિશ્ચિત રાસાયણિક પ્રક્રિયા $X \rightarrow Y$ માટે, નીપજના બનવાનો દર વિરુદ્ધ સમયનો ગ્રાફ (આલેખ) એ આકૃતિમાં દર્શાવેલ છે. નીચે આપેલામાંથી સાચાં વિધાન/નોની સંખ્યા $..............$ છે.View Solution
$(A)$ સમગ્ર પ્રક્રિયાનો ક્રમ છે.
$(B)$ આ પ્રક્રિયાનો ક્રમ શોધી શકાતો નથી.
$(C)$ $I$ અને $III$ વિભાગ માં, પ્રક્રિયા અનુક્રમે પ્રથમ અને શૂન્ય ક્રમની છે.
$(D)$ વિભાગ $II$ માં, પ્રક્રિયા પ્રથમક્રમની છે.
$(E)$ વિભાગ $II$ માં, પ્રક્રિયાનો ક્રમ $0.1$ થી $0.9$ વિસ્તાર માં છે.
- 7પ્રારંભિક પ્રકિયા $2AB + B \to A_2B_3$ એ પ્રકિયકોના સમાન મોલ લઇને $1\, dm^3$ અને $2\, dm^3$ કદના પાત્રોમાં અલગ રીતે કરવામાં આવે તો પ્રક્રિયાવેગનો ગુણોત્તર $(r_1/r_2$) ...View Solution
- 8પ્રક્રિયકની સાંદ્રતા $0.5\, M$ હોય ત્યારે પ્રથમ ક્રમની એક પ્રક્રિયાનો વેગ $1.5 \times 10^{-2}$ મોલ$^{-1}$ મિનિટ$^{-1}$ છે. તો પ્રક્રિયાનો અર્ધઆયુષ્ય સમય .......... મિનિટ છે.View Solution
- 9$NO_2 + CO \rightarrow CO_2 + NO,$ પ્રક્રિયા માટે દર સમીકરણ દર $= K [NO_2]^2$ તો ધીમા તબક્કામાં ભાગ લેતા $CO$ ના અણુઓની સંખ્યા કેટલી થશે?View Solution
- 10પ્રથમ ક્રમની વાયુમય પ્રક્રિયા માટે જ્યારે $\log \,k$ વિરૂદ્ધ $1/T $ નો આલેખ આપેલ છે. જેનો ઢાળ $-8000 $ સીધી રેખામાં મળે છે,તો પ્રક્રિયાની સક્રીયકરણ ઊર્જા ......... $cal$ શોધો.View Solution
