$27\, km/hr$ ની ઝડપથી જતી સબમરીન $(B)$ $18\, km/hr$ની ઝડપથી જતી સબમરીન $(A)$ નો પીછો કરે છે.$B$ $A$ ને શોધવા $500\, Hz$ નું સોનાર સિગ્નલ મોકલે છે અને $v$ આવૃતિનો અવાજ મેળવે છે.તો $v$ ની કિમત કેટલી ... $Hz$ હશે? (પાણીમાં ધ્વનિની ઝડપ $= 1500\, ms^{-1}$)
JEE MAIN 2019, Medium
Download our app for free and get started
b
\(v =\) speed of sound in water \(=1500 m / s\)
\(v =\) speed of sound in water \(=1500 m / s\)
frequency received by \(A = f\)
\(=\left[\frac{ V - V _{ A }}{ V - V _{ B }}\right] f _{0}=\left[\frac{1500-5}{1500-7.5}\right] f _{0}\)
frequency received by \(B = f ^{\prime \prime}=\)
\(\left[\frac{ V + V _{ B }}{ V + V _{ A }}\right] f ^{\prime}=\left[\frac{1500+7.5}{1500+5}\right]\left[ \frac{1500-5}{1500-7.5}\right] f\)
\(f ^{\prime \prime}=\left(\frac{1500+7.5}{1500-7.5}\right)\left(\frac{1500-5}{1500+5}\right)(500)\)
\(=502\; Hz\)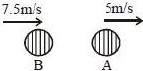
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$114\, cm$ લંબાઈ ધરાવતા સોનોમીટરના તારને બંને બાજુથી જડિત કરેલ છે. બે સોનોમીટરમાં બે ટેકા ક્યાં સ્થાને મૂકવાથી તે ત્રણ ભાગમાં વિભાજિત થાય કે જેથી તેમની મૂળભૂત આવૃતિનો ગુણોત્તર $1 : 3 : 4$ મળે?View Solution
- 2વાયોલીનની દોરી સાચા તણાવે $205 \,Hz$ નો નાદ છોડે છે. દોરીને થોડું વધારે તણાવ આપતા $205 \,Hz$ આવૃતિના સ્વરકાંટા સાથે બે સેકન્ડમાં છ સ્પંદ ઉત્પન્ન કરે છે. તરંગ દોરી વડે છોડાતા નાદની આવૃતિ ........ $Hz$ છે.View Solution
- 3લંબાઈ $L$ અને એકરૂપ ઘનતા વાળા લટકતાં દોરડાના નીચેના છેડ સ્પંદ ઉત્પન્ન કરવામાં આવે છે. જ્યારે આ સ્પંદ દોરડાના મધ્યબિંદુ પાસે પહોંચે છે ત્યારે સ્પંદની ઝડપ શોધો.View Solution
- 4ચામાચીડિયું $10\,ms^{-1}$ ના વેગથી દીવાલ તરફ $8000\,Hz$ આવૃતિવાળા ધ્વનિના તરંગો મોકલે છે. જે અથડાયને પાછો આવે ત્યારે ચામાચીડિયાને $f$ આવૃતિવાળા ધ્વનિના તરંગો સંભળાય છે. તો $f$ નું મૂલ્ય $Hz$માં કેટલું હશે? (ધ્વનિની ઝડપ$= 320\,ms^{-1}$ )View Solution
- 5દોરી પર ગતિ કરતાં તરંગ દ્વારા કણનું સ્થાનાંતર $x = A\, sin\, (2t -0.1\, x)$ મુજબ આપવામાં આવે છે. તો આ તરંગની તરંગલંબાઈ કેટલી હશે?View Solution
- 6એક સમાન તારનું એકમ લંબાઈ દીઠ દળ $0.135\, g / cm$ છે. ઉત્પન્ન થતાં લંબગ તરંગ ને $y=-0.21 \sin (x+30 t)$ દ્વારા દર્શાવવામાં આવે છે જ્યાં $x$ મીટર અને $t$ સેકન્ડમાં છે. તારમાં ઉત્પન્ન થતી તણાવનું અપેક્ષિત મૂલ્ય $x \times 10^{-2} N$ છે.$x$ નું મૂલ્ય ......... છે. (નજીકનાં પૂર્ણાક માટે શુન્યાંત મેળવો (Round-off))View Solution
- 7બંને છેડે ખુલ્લી હોય તેવી એક નળાકાર નળીની હવામાં મૂળભૂત આવૃત્તિ $f_0$ છે. આ નળીને પાણીમાં ઊભી ડૂબાડતા અડધી નળી સુધી પાણી ભરાય છે. હવે હવાનાં સ્તંભની મૂળભૂત આવૃત્તિ કેટલી થાય?View Solution
- 8પિયાનોની બે કળને એકસાથે દબાવવામાં આવે છે. તેના દ્વારા ઉત્પન્ન થતી આવૃતિ ${n_1}$ અને ${n_2}$ હોય તો દર સેકન્ડે કેટલા સ્પંદ સંભળાશે?View Solution
- 9$85\;cm$ લાંબી એક છેડેથી બંધ નળીના વાયુ સ્તંભ માટે $1250\; Hz$ થી ઓછી કેટલી પ્રાકૃતિક આવૃતિ મળે? (ધ્વનિનો વેગ $=340 \;m/s$)View Solution
- 10બે સ્વરકાંટાને એકસાથે કંપન કરાવતા $6$ સ્પંદ પ્રતિ સેકન્ડે સંભળાય છે,એક સ્વરકાંટાની આવૃત્તિ $341$ છે.બીજા સ્વરકાંટાને મીણ લગાવતાં સ્પંદની સંખ્યા $2$ પ્રતિ સેકન્ડ થાય છે,તો બીજા સ્વરકાંટાની આવૃત્તિ કેટલી થાય?View Solution