$4.5\times10^{-2}\,m$ બાજુની લંબાઈ ધરાવતા સમબાજુ ત્રિકોણની બાજુ પર $1\,A$ નો પ્રવાહ વહે છે.તો ત્રિકોણના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર $Wb/m^2$માં કેટલું મળે?
JEE MAIN 2018, Diffcult
a
Here, side of the triangle, \(l=4.5 \times 10^{-2} \,\mathrm{m}\) current, \(I =1 \,\mathrm{A}\)
Here, side of the triangle, \(l=4.5 \times 10^{-2} \,\mathrm{m}\) current, \(I =1 \,\mathrm{A}\)
magnetic field at the centre of the triangle \('O'B = ?\)
From figure, \(\tan 60^{\circ}=\sqrt{3}=\frac{1}{2 d}\)
\(\Rightarrow d=\frac{l}{2 \sqrt{3}}=\left(\frac{4.5 \times 10^{-2}}{2 \sqrt{3}}\right)\, \mathrm{m}\)
Magnetic field, \(B=\frac{\mu_{0} i}{4 \pi d}\left(\cos \theta_{1}+\cos \theta_{2}\right)\)
Putting value of \(\mu=4 \pi \times 10^{-7}\) and \(\theta_{1}\) and \(\theta_{2}\)
we will get net magenetic field
\(=3 \times B=4 \times 10^{-5} \,\mathrm{Wb} / \mathrm{m}^{2}\)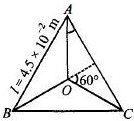
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પાતળા એકસમાન વાહક તાર પર અવાહકનું પડ ચડાવેલ છે. એક તારને વાળીને લૂપ બનાવવામાં આવે છે જેમાંથી $I$ પ્રવાહ પસાર કરતાં તે તેના કેન્દ્ર આગળ $B_1$ ચુંબકીય ક્ષેત્ર ઉત્પન્ન કરે છે. બીજા તારમાંથી ત્રણ સમાન લૂપ બનાવીને એકબીજાની પાસે મૂકવામાં આવે છે. જેમાંથી $I/3$ પ્રવાહ પસાર કરતાં તેના કેન્દ્ર આગળ $B_2$ ચુંબકીય ક્ષેત્ર ઉત્પન્ન કરે છે, તો $B_1 : B_2$ નો ગુણોત્તર કેટલો મળે?View Solution
- 2View Solutionસઇક્લોટ્રોન કોને પ્રવેગિત કરવામાં વપરાય છે?
- 3$5 \mathrm{eV}$ ગતિઊર્જા ધરાવતો એક ઈલેકટ્રોન $3 \mu \mathrm{T}$ ના નિયમિત ચુંબકીય ક્ષેત્ર ધરાવતા વિસ્તારમાં ક્ષેત્રની દિશાને લંબરૂપે દાખલ થાય છે. $E$ જેટલું વિદ્યુતક્ષેત્ર વેગની દિશા અને ચુંબકીય ક્ષેત્રની દિશાને લંબરૂપે લગાવવામાં આવે છે. ઇલેકટ્રોન ત જ માર્ગ ઉપર ગતિ ચાલુ રાખે તે માટે જરૂરી $E$નું મૂલ્ય. . . . . . $\mathrm{NC}^{-1}$ થશે. (ઇલેકટ્રોનનું દળ = $9 \times 10^{-31} \mathrm{~kg},$ ઈલેકટ્રોનનો વિદ્યુતભાર $= 1.6 \times 10^{-19} \mathrm{C}$ આપેલ છે.)View Solution
- 4$q$ વિદ્યુતભાર અને $m$ દળ ધરાવતો કણ $x-$ અક્ષની દિશામાં $v$ વેગથી ગતિ કરે છે.તો કઇ આકૃતિમાં ઇલેકટ્રોન વિચલન થયા વગર પસાર થશે?View Solution
- 5એકમ દળ દીઠ વિદ્યુતભાર $\alpha$ ધરાવતો એક કાણ ઉદગમથી વેગ $\bar{v}=v_0 \hat{i}$ સાથે એકરૂપ ચુંબકીય ક્ષેત્ર $\bar{B}=-B_0 \hat{k}$ માં છોડવામાં આવે છે, જો કણ $(0, y, 0)$ માંથી પસાર થાય, તો $y$ બરાબરView Solution
- 6એક એકરૂપ સુવાહક તાર $A B C$ નું દળ $10\,g$ છે. તેમાંથી $2\,A$નો વિદ્યુતપ્રવાહ પસાર થાય છે. તારને એક્સમાન ચુંબકીય ક્ષેત્ર $B=2\,T$ માં રાખેલ છે. તારનો વેગ ........... $ms ^{-2}$ હશે.View Solution
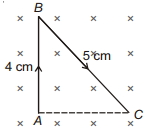
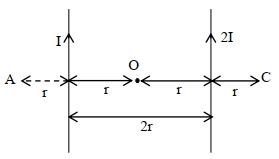
- 7બાજુમાં દર્શાવેલ આકૃતિમાં દર્શાવ્યા અનુસાર બે સમાંતર લાંબા વિદ્યુતપ્રવાહ ધરાવતા તારને $2 r$ અંતરે રાખવામાં આવ્યા છે. બિંદુ $A$ આગળ ચુંબકીય ક્ષેત્ર અને $C$ આગળ ઉત્પન ચુંબકીય ક્ષેત્ર વચ્ચેનો ગુણોતર $\frac{x}{7} $ છે. $x$ નું મૂલ્ચ. . . . . . થશે.View Solution
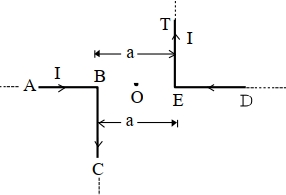
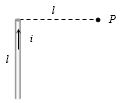
- 8આપેલ આકૃતિ માં $P $ બિંદુએ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 9એક emf $90\,V$ ની બેટરીને $100\,\Omega$ ના બે આવરોધોના શ્રેણી જોડાણ સાથે લગાડેલ છે. $400\,\Omega$ આંતરિક અવરોધનું એક વોલ્ટમીટર પ્રત્યેક અવરોધના છેડા વચ્ચે સ્થિતિમાન તફાવત માપવા માટે વપરાય છે. તો વોલ્ટ મીટરનું આવલોકન $.........$ હોય.View Solution
- 10આકૃતિમાં દર્શાવેલ વીજપ્રવાહની ગોઠવણી માટે $O$ બિંદુએ ચુંબકીય પ્રેરણનું મૂલ્યView Solution