બે પાતળા એકસમાન વાહક તાર પર અવાહકનું પડ ચડાવેલ છે. એક તારને વાળીને લૂપ બનાવવામાં આવે છે જેમાંથી $I$ પ્રવાહ પસાર કરતાં તે તેના કેન્દ્ર આગળ $B_1$ ચુંબકીય ક્ષેત્ર ઉત્પન્ન કરે છે. બીજા તારમાંથી ત્રણ સમાન લૂપ બનાવીને એકબીજાની પાસે મૂકવામાં આવે છે. જેમાંથી $I/3$ પ્રવાહ પસાર કરતાં તેના કેન્દ્ર આગળ $B_2$ ચુંબકીય ક્ષેત્ર ઉત્પન્ન કરે છે, તો $B_1 : B_2$ નો ગુણોત્તર કેટલો મળે?
JEE MAIN 2014, Diffcult
b
For loop \(\mathrm{B}=\frac{\mu_{0} \mathrm{nI}}{2 \mathrm{a}}\)
For loop \(\mathrm{B}=\frac{\mu_{0} \mathrm{nI}}{2 \mathrm{a}}\)
where, \(a\) is the radius of loop.
Then, \(B_{1}=\frac{\mu_{0} I}{2 a}\)
Now, for coil \(\mathrm{B}=\frac{\mu_{0} \mathrm{I}}{4 \pi} \cdot \frac{2 \mathrm{nA}}{\mathrm{x}^{3}}\)
at the centre \(x=\) radius of loop
\(\mathrm{B}_{2} =\frac{\mu_{0}}{4 \pi} \cdot \frac{2 \times 3 \times(1 / 3) \times \pi(\mathrm{a} / 3)^{2}}{(\mathrm{a} / 3)^{3}} \)
\(=\frac{\mu_{0} \cdot 3 \mathrm{I}}{2 \mathrm{a}} \)
\(\therefore \frac{B_{1}}{B_{2}}=\frac{\mu_{0} I / 2 a}{\mu_{0} \cdot 3I / 2 a}\)
\(B_{1}: B_{2}=1: 3\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$X-Z$ સમતલમાં ઉગમબિંદુ પર એક એક લંબચોરસ ($5\,cm\times 2\,cm$) $100\,$ આંટાવાળા ગુચળામાથી $3\,A$ પ્રવાહ સમઘડી દિશામાં વહે છે.$X$ અક્ષની દિશામાં $1\,T$ ચુંબકીય ક્ષેત્ર પ્રવર્તે છે.જો ગૂચળાંને $Z$ અક્ષ સાથે $45^o$ના ખૂણે વાળવામાં આવે તો તેના પર કેટલા ......$Nm$ ટોર્ક લાગે?View Solution
- 2બે વર્તુળાકાર ગૂંચળા $1$ અને $2$ સમાન તારમાંથી બનાવેલ છે પરંતુ પ્રથમ ગૂંચળાની ત્રિજયા બીજા ગૂંચળા કરતાં બમણી છે. તેમની વચ્ચે લગાવવા પડતાં સ્થિતિમાનના તફાવતનો ગુણોત્તર કેટલો હોવો જોઈએ કે જેથી તેમના કેન્દ્ર પર સમાન ચુંબકીયક્ષેત્ર ઉત્પન્ન થાય?View Solution
- 3સમાન દળ ધરાવતા બે આયનોના વિદ્યુતભારનો ગુણોત્તર $1: 2$ છે. તેમને સમાન ચુંબકીયક્ષેત્રમાં લંબરૂપે $2: 3$ ઝડપના ગુણોત્તરે દાખલ કરવામાં આવે છે. તેમની વર્તુળાકાર ત્રિજ્યાનો ગુણોત્તર કેટલો થાય?View Solution
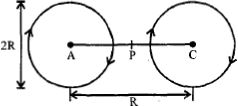
- 4$N$ આંટા અને $R$ ત્રિજ્યા ધરાવતા હેલ્મહોલ્ટ્જ ગુચળાની જોડ આપેલ છે. તે એક બીજાથી $R$ અંતરે છે.અને તેમાંથી સમાન પ્રવાહ $I$ સમાન દિશામાં વહે છે. તો કેન્દ્ર $A$ અને $C$ ને જોડતી રેખા પરના મધ્યમાં રહેલ બિંદુ $P$ આગળ ચુંબકીયક્ષેત્રનું મૂલ્ય કેટલું મળે?View Solution
- 5View Solutionબોહરનાં મેગ્નેટોન માટે (સંજ્ઞાઓનાં સામાન્ય અર્થમાં છે.)
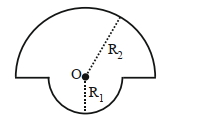
- 6આકૃતિમાં દર્શાંવ્યા અનુસાર, $\mathrm{I}=4 \mathrm{~A}$ નો પ્રવાહ ધરાવતી અને $\mathrm{R}_1=2 \pi$ મીટર અને $\mathrm{R}_2=4 \pi$ મીટરની ત્રિજ્યા ધરાવતા બે અર્ધવર્તુળાકાર ગાળાના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર $\alpha \times 10^{-7}$ ટેસ્લા છે. (દરેક ભાગ માટે કેન્દ્ર $\mathrm{O}$ છે.)View Solution
- 7બે અર્ધવર્તુળાકાર $R$ ત્રિજયાના ભાગની બનેલ એક પ્રવાહધારીત લૂપનો એક ભાગ $xy$ સમતલમાં અને બીજો ભાગ $xz$ સમતલમાં છે. જો તેમાંથી $I$ પ્રવાહ પસાર થાય છે. બે અર્ધવર્તુળાકાર ભાગના કારણે તેમના સામાન્ય કેન્દ્ર પર પરિણામી ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
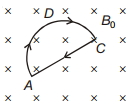
- 8આકૃતિમાં એકરૂપ ચુંબકીય ક્ષેત્ર $B_0$ ના વિસ્તારમાં મૂકેલી અને વિદ્યુતપ્રવાહ $i$ ધરાવતી સુવાહક રીંગ $A D C A$ દર્શાવેલ છે. અર્ધવર્તુળ ભાગ પર લાગતા બળનું મૂલ્ય કેટલું છે ?View Solution
- 9View Solutionએક વિસ્તારમાં સ્થિર અને સમાન વિદ્યુતક્ષેત્ર અને ચુંબકીયક્ષેત્ર છે. આ બંને ક્ષેત્રો સમાંતર છે. એક સ્થિર વિદ્યુભારિત કણ આ વિસ્તારમાં મુક્ત કરવામાં આવે છે. તો આ કણનો ગતિમાર્ગ.......
- 10View Solutionચુંબકીયક્ષેત્ર વિરુધ્ધ ઊર્જા ઘનતાનો આલેખ કેવો થાય?
