$4\,cm$ ત્રિજ્યાનો સાબુનો પરપોટો બીજા $6\,cm$ ત્રિજ્યાના પરપોટામાં તેને સંપર્ક કર્યા સીવાય ફસાયેલ છે.$P_2$ એ અંદરના પરપોટાની અંદરનું દબાણ અને $P_0$ એ બહારના પરપોટાની બહારનું દબાણ છે.બીજા એક પરપોટોની ત્રિજ્યા જેની અંદર બહારના દબાણનો તફાવત $P_2 - P_0$ હોય? ....... $cm$
JEE MAIN 2018, Diffcult
d
Clearly from figure,
Clearly from figure,
\({P_2} = {P_0} + \frac{{4T}}{6} + \frac{{4t}}{4}\)
\(or,\,\,\,{P_2} - {P_0} = \frac{{4T}}{6} + \frac{{4T}}{4}\) \(...\left( i \right)\)
Let \(r\) be the radius of bubble with pressure difference
\({P_2} - {P_0}\,so,\)
\({P_2} - {P_0} = \frac{{4T}}{r}\) \(...(ii)\)
\(From\,e{q^n}\,\left( i \right)\,and\,\left( {ii} \right),\)
\(\frac{{4T}}{r} = \frac{{4T}}{6} + \frac{{4T}}{4}\)
\(\frac{1}{r} = \frac{1}{6} + \frac{1}{4} \Rightarrow r = 2.4\,cm\)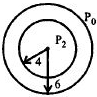
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન ત્રિજયા, $l_1$ અને $l_2$ લંબાઇ ધરાવતી કેશનળીને પાત્રના તળિયે સમાંતરમાં લગાવવામાં આવે છે,બંને કેશનળીની જગ્યાએ કેટલી લંબાઇની કેશનળી મૂકતાં પ્રવાહ સમાન રહે?View Solution
- 2પૃથ્વી પર પાણીમાં કેશનળી શિરોલંબ ડુબાડતાં $h$ ઊંચાઇ સુધી પાણી ઉપર ચડે છે.તો ચંદ્ર પર પાણીમાં કેશનળી શિરોલંબ ડુબાડતાં કેટલી ઊંચાઇ સુધી પાણી ઉપર ચડે ?View Solution
- 3$4.5 \mathrm{~cm}$ ત્રિજ્યા ધરાવતી એક પાતળી સપાટ વર્તુળાકાર તક્તીને પાણીની સપાટી ઉપર હળવેકથી મૂકવામાં આવે છે: જો પાણીનું પ્રુષ્ઠાતાણ $0.07 \mathrm{~N} \mathrm{~m}^{-1}$ હોય, તો તેને સપાટીથી દૂર કરવા માટે જરુરી વધારાનું બળ. . . . . . . થશે.View Solution
- 4કેશનળીને પાણીમાં ડુબાડતાં $h$ ઊંચાઇ સુધી પાણી ઉપર આવે છે.જો અડધી ત્રિજયાની કેશનળીને પાણીમાં ડુબાડતાં કેટલી ઊંચાઇ સુધી પાણી ઉપર આવે?View Solution
- 5View Solutionવિધાન : નાના ટીપાં મોટા ટીપાં કરતાં વધારે પ્રતિબળનો વિરોધ કરે.
કારણ : ટીપાની અંદરનું દબાણ તેની સપાટીના ક્ષેત્રફળના સમપ્રમાણમાં હોય
- 6$0.15\, mm$ ત્રિજ્યાવાળી કાંચમાંથી બનાવેલ એક કેશનળીને મિથિલિન આયોડાઇડમાં (પૃષ્ઠતાણ $=0.05\, Nm ^{-1},$ ઘનતા $\left.=667\, kg m ^{-3}\right)$ શિરોલંબ ડૂબાડતા નળી $h$ ઊંચાઈ સુધી ભરાઈ છે. પ્રવાહી અને કાંચ વચ્ચેની સપાટી (કેશનળીની બંને વિરુદ્ધ બાજુ) સાથે દોરેલા સ્પર્શક વચ્ચેનો ખૂણો $60^{\circ}$ છે. તો ઊંચાઈ $h(m$ માં) કેટલી હશે?View Solution
$\left(g=10\, ms ^{-2}\right)$
- 7$1\,cm$ ત્રિજયાના ટીપાંમાંથી સમાન ત્રિજયાના $1000$ ટીપાં બનાવવા માટે કેટલું કાર્ય કરવું પડે? પ્રવાહીનું પૃષ્ઠતાણ $50\, dynes/cm $ છે.View Solution
- 8બે પરપોટાની ત્રિજયા $r_1$ અને $r_2$ છે. શૂન્યઅવકાશમાં સમતાપીય સ્થિતિમાં ભેગા થઇને મોટો પરપોટો બનાવે,તો મોટા પરપોટાની ત્રિજયા કેટલી થાય?View Solution
- 9View Solutionમશીન દ્વારા પરપોટા બનાવવામાં આવે છે. મશીન પરપોટાની ત્રિજયા સમયના સપ્રમાણમાં વધારતું હોય,તો પરપોટાનું અંદરનું દબાણ વિરુધ્ધ સમયનો આલેખ કેવો થાય?
- 10$L$ બાજુવાળી ચોરસ ફ્રેમ પર $T$ પૃષ્ઠતાણ ધરાવતા સાબુના દ્રાવણનું પડ હોય,તો ફ્રેમ પર કેટલું બળ લાગે?View Solution
