$80 \,cm$ લંબાઈના એક સોલેનોઈડ પર પાસ-પાસે દરેક $400$ આંટા વાળા $5$ આવરણ વિંટાળ્યા છે. સોલેનોઈડનો વ્યાસ $1.8 \,cm$ છે. જો સોલેનોઈડમાં $8.0 \,A$ વિદ્યુતપ્રવાહ વહેતો હોય, તો તેના કેન્દ્ર પાસે $B$ નું મૂલ્ય શોધો.
Easy
a
Length of the solenoid, \(l=80\, cm =0.8 \,m\)
Length of the solenoid, \(l=80\, cm =0.8 \,m\)
There are five layers of windings of \(400\) turns each on the solenoid.
\(\therefore\) Total number of turns on the solenoid, \(N=5 \times 400=2000\)
Diameter of the solenoid, \(D=1.8 \,cm =0.018\, m\)
Current carried by the solenoid, \(I=8.0 \,A\)
Magnitude of the magnetic field inside the solenoid near its centre is given by the relation,
\(B=\frac{\mu_{0} N I}{l}\)
Where,
\(\mu_{0}=\) Permeability of free space \(=4 \pi \times 10^{-7}\, T\,m \,A ^{-1}\)
\(B=\frac{4 \pi \times 10^{-7} \times 2000 \times 8}{0.8}\) \(=8 \pi \times 10^{-3}=2.512 \times 10^{-2}\, T\)
Hence, the magnitude of the magnetic field inside the solenoid near its centre is \(2.512 \times 10^{-2}\; T\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
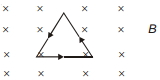
- 1એક તારને $100\,cm$ બાજુના સમભૂજ ત્રિકોણના સ્વરૂપમાં વાળવામાં આવ્યો છે અને $2\;A$ નો વિદ્યુતપ્રવાહ તેમાંથી વહે છે. તેને કાગળના સમતલની અંદર લંબ દિશામાં $2.0\,T$ પ્રેરણના ચુંબકીયક્ષેત્રમાં મૂકવામાં આવ્યો છે. ત્રિકોણની દરેક બાજુ પર લાગતા બળનું મૂલ્ય અને દિશા કેટલી હશે ?View Solution
- 2$5 \mathrm{eV}$ ગતિઊર્જા ધરાવતો એક ઈલેકટ્રોન $3 \mu \mathrm{T}$ ના નિયમિત ચુંબકીય ક્ષેત્ર ધરાવતા વિસ્તારમાં ક્ષેત્રની દિશાને લંબરૂપે દાખલ થાય છે. $E$ જેટલું વિદ્યુતક્ષેત્ર વેગની દિશા અને ચુંબકીય ક્ષેત્રની દિશાને લંબરૂપે લગાવવામાં આવે છે. ઇલેકટ્રોન ત જ માર્ગ ઉપર ગતિ ચાલુ રાખે તે માટે જરૂરી $E$નું મૂલ્ય. . . . . . $\mathrm{NC}^{-1}$ થશે. (ઇલેકટ્રોનનું દળ = $9 \times 10^{-31} \mathrm{~kg},$ ઈલેકટ્રોનનો વિદ્યુતભાર $= 1.6 \times 10^{-19} \mathrm{C}$ આપેલ છે.)View Solution
- 3View Solutionસોલેનોઇડમાં ચુંબકીયક્ષેત્રનો છેડાથી અંતરની સાથે થતો ફેરફાર ક્યો ગ્રાફ દર્શાવે છે?
- 4$25$ આંટા અને $10$ સેમી વ્યાસ ધરાવતી કોઇલમાંથી $4$ એમ્પિયર પ્રવાહ પસાર થાય છે,તો કોઇલનાં કેન્દ્ર પર ચુંબકીય ક્ષેત્ર શું થશે?View Solution
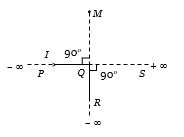
- 5અનંત લંબાઇના $PQR$ તારને કાટખૂણે વાળીને $I$ પ્રવાહ પસાર કરતાં $M$ બિંદુએ ચુંબકીયક્ષેત્ર $H_1$ છે.હવે,બીજા અનંત લંબાઇના $QS$ તારને આકૃતિ મુજબ જોડતાં $QS$ માં $I/2$ પ્રવાહ પસાર થાય છે.હવે $M$ બિંદુએ ચુંબકીયક્ષેત્ર $ {H_{2}} $ છે,તો $ \frac{H_1}{H_2} $ કેટલું થાય?View Solution
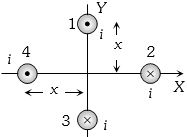
- 6$R$ જેટલી સમાન ત્રિજયા ધરાવતી બે રિંંગોના સમતલ એકબીજાને લંબ હોય તેમ સમકેન્દ્રીય છે. તેમના વહેતા વિદ્યુતપ્રવાહો અનુક્રમે $I$ અને $2I$ છે. તેમના કેન્દ્ર પર પરિણામી પ્રેરિત ચુંબકીયક્ષેત્ર કેટલું હશે?View Solution
- 7ચાર અનંત લંબાઇના તારથી ઉદ્ગમબિંદુ પર પરિણામી ચુંબકીયક્ષેત્ર કેટલું થાય? દરેક તાર ઉદ્ગમબિંદુ પર $B$ ચુંબકીયક્ષેત્ર ઉત્પન્ન કરે છે.View Solution
- 8$i$ પ્રવાહવાળા $d\vec l$ લંબાઇના ખંડથી $\vec r$ અંતરે ચુંબકીયક્ષેત્ર $d\overrightarrow B$ કેટલું થાય?View Solution
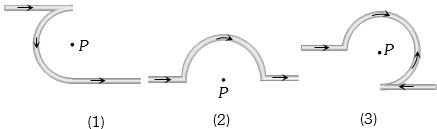
- 9નીચેની આકૃતિમાં $P$ બિંદુ આગળ ચુંબકીયક્ષેત્રનો ગુણોત્તર કેટલો થાય?View Solution
- 10એક પ્રોટોન અને એક $\alpha-$કણ (તેમનાં દ્રવ્યમાનનો ગુણોત્તર $1:4$ અને વિધુતભારનો ગુણોત્તર$1: 2$) સ્થિર સ્થિતિમાંથી $V$ વિજસ્થિતિમાનના તફાવતથી પ્રવેગીત કરવામાં આવે છે. જો તેમની ગતિઓને લંબ એકસમાન ચુંબકીય ક્ષેત્ર $(B) $ પ્રસ્થાપિત કરવામાં આવે, તો તેઓ વડે કપાતા વર્તુળાકાર પથની ત્રિજ્યાઓનો ગુણોત્તર $r_p : r_{\alpha }$ કેટલો થશે?View Solution
