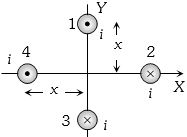
ચાર અનંત લંબાઇના તારથી ઉદ્ગમબિંદુ પર પરિણામી ચુંબકીયક્ષેત્ર કેટલું થાય? દરેક તાર ઉદ્ગમબિંદુ પર $B$ ચુંબકીયક્ષેત્ર ઉત્પન્ન કરે છે.

Diffcult
c
(c) Direction of magnetic field (\(B_1, B_2, B_3\, and \,B_4\)) at origin due to wires \(1\), \(2\), \(3\) and \(4\) are shown in the following figure.
(c) Direction of magnetic field (\(B_1, B_2, B_3\, and \,B_4\)) at origin due to wires \(1\), \(2\), \(3\) and \(4\) are shown in the following figure.
\({B_1} = {B_2} = {B_3} = {B_4} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2i}}{x} = B\).
So net magnetic field at origin \(O\) \({B_{net}} = \sqrt {{{({B_1} + {B_3})}^2} + {{({B_2} + {B_4})}^2}} \)\( = \sqrt {{{(2B)}^2} + {{(2B)}^2}} = 2\sqrt 2 \,B\)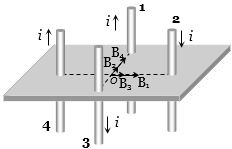
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએક સમાન ચુંબકીય ક્ષેત્રમાં વર્તુળાકાર ગતિ કરતાં વિદ્યુતભારનો આવર્તકાળ કોનાથી સ્વતંત્ર હોય?
- 2$50\,\Omega $ અવરોધ ધરાવતું ગેલ્વોનોમીટર પૂર્ણ આવર્તન દરમિયાન $4\,mA$ પ્રવાહ દર્શાવે છે.આ ગેલવેનોમીટરને $5\,k\Omega $ અવરોધ જોડીને વોલ્ટમીટરમાં ફેરવેલ છે તો આ વોલ્ટમીટર કેટલા......$V$ વૉલ્ટ સુધીનો વૉલ્ટેજ માપી શકશે?View Solution
- 3$80 \,cm$ લંબાઈના એક સોલેનોઈડ પર પાસ-પાસે દરેક $400$ આંટા વાળા $5$ આવરણ વિંટાળ્યા છે. સોલેનોઈડનો વ્યાસ $1.8 \,cm$ છે. જો સોલેનોઈડમાં $8.0 \,A$ વિદ્યુતપ્રવાહ વહેતો હોય, તો તેના કેન્દ્ર પાસે $B$ નું મૂલ્ય શોધો.View Solution
- 4એક સુરેખ તારમાંથી $ I$ પ્રવાહ પસાર થાય છે.તેમાંથી એક આંટાવાળી રીંગ બનાવતા કેન્દ્ર પાસે ચુંબકીયક્ષેત્ર $B$ છે.જો તેમાંથી ત્રણ આંટાવાળી રીંગ બનાવતા કેન્દ્ર પાસે ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
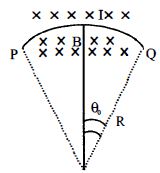
- 5ચુંબકીયક્ષેત્ર $B$ (કાગળના સમતલને લંબ $\times \times \times $ વડે દર્શાવેલ છે) માં એક તારને $R$ ત્રિજયા ધરાવતી ચાપ તરીકે $P$ અને $Q$ બિંદુ વચ્ચે જડિત કરેલ છે. જેમાંથી પ્રવાહ $I$ પસાર થાય છે. તો તારથી બનેલ ચાપ કેન્દ્ર સાથે $2\theta_0$ નો ખૂણો બનાવતી હોય તો તારમાં તણાવ કેટલું હશે?View Solution
- 6જ્યારે બે ગુંચળામાંથી સમાન વિદ્યુત પ્રવાહ પસાર થાય છે. ત્યારે તેના કેન્દ્ર પાસે સમાન ચુંબકીય ક્ષેત્ર ઉત્પન્ન થાય છે. જો ગૂંચળાઓમાં આંટાઓની સંખ્યાનો ગુણોતર $8 : 15$ હોય,તો તેની ત્રિજ્યાનો ગુણોત્તર કેટલો હશે ?View Solution
- 7વર્તુળાકાર આડછેદ અને સ્થિત વિદ્યુતપ્રવાહ ઘરાવતા લાંબા સીધા તાર માટના એમ્પિયર પરિપથીય નિયમ $(circuital\, law)$ થી તારના અંદરના અને બહારના વિસ્તારમાં ચુંબકીય ક્ષેત્રનો ફેરફાર$.....$View Solution
- 8$m$ દળ અને $Q$ વિદ્યુતભારનો વિદ્યુતભરીત કણ $r$ ત્રિજ્યાના વર્તુળાકાર પથ પર ચુંબકીય ક્ષેત્ર $B$ને લંબ ગતિ કરે છે તો તેનો આવર્તકાળ કેટલો થાય?View Solution
- 9પ્રોટોન અને $\alpha$ ની ગતિઉર્જા $K _{ p }$ અને $K _{\alpha}$ છે. તે ચુંબકીયક્ષેત્રમાં લંબ દાખલ થતાં ત્રિજ્યાના ગુણોતર $2: 1 $ છે તો ગતિઉર્જાનો ગુણોતર $K _{ p }: K _{\alpha}$ શું હશેView Solution
- 10$1 \Omega$ નો અવરોધ, $2 \times 10^{-6} \Omega \mathrm{m}$, ની અવરોધક્તા, $10 \mathrm{~mm}^2$ નું આડછેદનું ક્ષેત્રફળ અને $500 \mathrm{~g}$ દળ ધરાવતા એક ધાતુના સીધા તારમાંથી $2 A$ પ્રવાહ પસાર થાય છે. તેને નિયમિત ચુંબકીય ક્ષેત્ર $\vec{B}$ ની મદદથી હવામાં મધ્યમાં સમક્ષિતિજ રીતે લટકવવામાં આવે છે. $B$ નું મૂલ્ય. . . . . . . . . $\times 10^{-1} \mathrm{~T}$ છે. $\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\right.$ છે. )View Solution
