$900 Kg/m^3$ ઘનતા ધરાવતો બરફનો ટુકડો $1000 Kg/m^3 $ ઘનતા ધરાવતા પાણીમાં તરે છે,બરફનું ....... $\%$ કદ પાણીની બહાર રહે .
Diffcult
c
(c) Let the total volume of ice-berg is \(V\) and its density is \(\rho\). If this ice-berg floats in water with volume Vin inside it then \({V_{in}}\sigma g = V\rho g\) ==> \({V_{in}} = \left( {\frac{\rho }{\sigma }} \right)\;V\)[\(\sigma = \)density of water]
or \({V_{out}} = V - {V_{in}} = \left( {\frac{{\sigma - \rho }}{\sigma }} \right)\;V\)
==> \(\frac{{{V_{out}}}}{V} = \left( {\frac{{\sigma - \rho }}{\sigma }} \right) = \frac{{1000 - 900}}{{1000}} = \frac{1}{{10}}\)
\({V_{out}} = 10\% \) of \(V\)
(c) Let the total volume of ice-berg is \(V\) and its density is \(\rho\). If this ice-berg floats in water with volume Vin inside it then \({V_{in}}\sigma g = V\rho g\) ==> \({V_{in}} = \left( {\frac{\rho }{\sigma }} \right)\;V\)[\(\sigma = \)density of water]
or \({V_{out}} = V - {V_{in}} = \left( {\frac{{\sigma - \rho }}{\sigma }} \right)\;V\)
==> \(\frac{{{V_{out}}}}{V} = \left( {\frac{{\sigma - \rho }}{\sigma }} \right) = \frac{{1000 - 900}}{{1000}} = \frac{1}{{10}}\)
\({V_{out}} = 10\% \) of \(V\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ટાંકીમાંથી એક પંપ વડે પાણી ખેંચવામાં આવે છે અને જેને પાણી જ્યાંથી ખેંચવામાં આવે છે તેનાથી $2.5\; m$ શિરોલંબ ઉંચાઈએ આવેલા હોઝના અંત ભાગમાં પહોંચાડવામાં આવે છે તેના આડછેદનું ક્ષેત્રફળ $10 \;cm^2$ છે અને હોઝના અંતમાં પાણીને $5 \;m/s$ ની ઝડપથી છોડવામાં આવે છે. કાર્યરત પંપના પાવરનો દર ......... $W$ હશે .View Solution
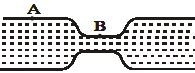
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે એક સમક્ષિતિજ નળીમાંથી પાણી વહે છે. $\mathrm{A}$ અને $\mathrm{B}$ બિંદુ જેમના આડછેડના ક્ષેત્રફળ અનુક્રમે $40\; \mathrm{cm}^{2}$ અને $20\; \mathrm{cm}^{2}$ છે, તેમની વચ્ચે દબાણનો તફાવત $700\; \mathrm{Nm}^{-2}$ છે.તો નળીમાંથી દર સેકન્ડે પસાર થતાં પાણીનું કદ . ........ $\mathrm{cm}^{3} / \mathrm{s}$ હશે.View Solution
- 3હવામાં $3 \,kg$ વજનના ધાતુના ગોળાને દોરી વડે એવી રીતે લટકાડવામાં આવે છે કે તે $0.8$ સાપેક્ષ ઘનતા ધરાવતા પ્રવાહીમાં સંપૂર્ણ ડૂબેલો રહે. ધાતુની સાપેક્ષ ઘનતા $10$ છે તો દોરીમાં તણાવ ......... $N$ છે.View Solution
- 4$1.2$ ઘનતા ધરાવતા એક બિકરમાં બરફનો ટુકડો તરે છે જ્યારે તે સંપૂર્ણ ઓગળી જાય ત્યારે પ્રવાહીની સપાટી .....View Solution
- 5પાણીના આઠ ટીપાંઓ $10\,cm / s$ ની અચળ ઝડપે હવામાંથી પાણીમાં પડે છે. જો ટીપાંઓ જોડાય તો તેનો નવો વેગ $.......cm/s$ છે.View Solution
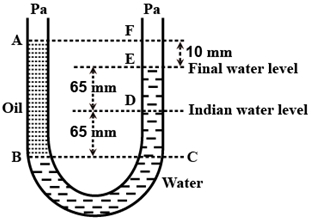
- 6એક $U$ નળી જેના બંને છેડાઓ વાતાવરણ તરફ ખુલ્લા છે, તે આંશિક રીતે પાણીથી ભરેલા છે. પાણી સાથે ન ભળી જાય તેવું તેલ નળીના એક બાજુમાં ત્યાં સુધી ભરવામાં આવે છે, જયાં સુધી બીજી બાજુમાં આવેલા પાણીની સપાટીથી $10\;mm$ ઊંચાઇ પ્રાપ્ત કરી લે છે. આ દરમિયાન પાણી પોતાનો સ્તર $65 \;mm$ જેટલું વધે છે (આકૃતિ જુઓ). તેલની ઘનતા ($kg/m^3$ માં) કેટલી હશે?View Solution
- 7View Solutionવિધાન : પ્રેશરકૂકરમાં પાણી ગરમ કરવામાં આવે છે.હવે કૂકરને સ્ટવ પરથી દૂર કરવામાં આવે છે. હવે કૂકરનું ઢાકનું ખોલતા પાણી પાછું ગરમ થવા લાગે છે.
કારણ : પાણીમાં રહેલ અશુદ્ધિ તેનું ઉત્કલનબિંદુ ઘટાડે છે.
- 8પાત્રના તળિયે $l$ લંબાઇ અને $r$ ત્રિજયા ઘરાવતી કેશનળી જોડેલ છે.તેના પર દબાણનો તફાવત $P$ હોય,ત્યારે બહાર આવતા પાણીનું કદ $V$ છે,હવે તેની સાથે શ્રેણીમાં સમાન લંબાઇ પરંતુ અડધી ત્રિજયા ધરાવતી કેશનળી જોડતાં બહાર આવતાં પ્રવાહીનું કદ ( તંત્ર વચ્ચે દબાણનો તફાવત $P$ છે. )View Solution
- 9તાર વડે લટકાવેલો એક પદાર્થ તેને $10 \,mm$ જેટલો ખેંચે છે, જ્યારે પદાર્થને પ્રવાહીમાં ડૂબાડવામાં આવે છે ત્યારે તારમાં ખેંચાણા $\frac{10}{3} \,mm$ જેટલું ઘટે છે તો પદાર્થ અને પ્રવાહીની સાપેક્ષ ઘનતાઓનો ગુણોત્તર કેટલો છે ?View Solution
- 10દરિયાની આશરે ઊંડાઇ $2700 \;m$ છે. પાણીની દબનીયતા $45.4\times 10^{-11} \;Pa^{-1}$ અને પાણીની ઘનતા $10^3 \;kg\,m^{-3}$ છે. દરિયાના તળિયે રહેલા પાણીની આંશિક કદ વિકૃતિ કેટલી હશે?View Solution
