A 13-m-long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
Let AB be the building and CB be the ladder. Then, $\text{AB}=12\text{m},\text{CB}=13\text{m}$ and $\angle\text{CAB}=90^\circ$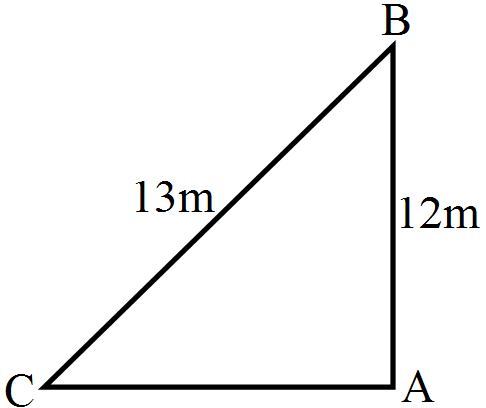
By Pythagoaras theoram, we have $\text{CB}^2=\text{AB}^2+\text{AC}^2$ $\text{AC}^2=\big[\text{CB}^2-\text{AB}^2\big]$ $=\Big[(13)^2-(12)^2\Big]\text{m}^2$ $=(169-144)\text{m}^2$ $=25\text{m}^2$ $\Rightarrow\text{AC}=\sqrt{25}\text{m}=5\text{m}$ Hence, the distance of the fool of the ladder from the building is 5m.

By Pythagoaras theoram, we have $\text{CB}^2=\text{AB}^2+\text{AC}^2$ $\text{AC}^2=\big[\text{CB}^2-\text{AB}^2\big]$ $=\Big[(13)^2-(12)^2\Big]\text{m}^2$ $=(169-144)\text{m}^2$ $=25\text{m}^2$ $\Rightarrow\text{AC}=\sqrt{25}\text{m}=5\text{m}$ Hence, the distance of the fool of the ladder from the building is 5m.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1A guy wire attached to a vertical pole of height $18\ m$ is $24\ m$ long and has a stake attached to the other end.View Solution
How far from the base of the pole should the stake be driven so that the wire will be taut? - 2In the given figure, D is the midpoint of side BC and $\text{AE}\perp\text{BC}.$ If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that.View Solution
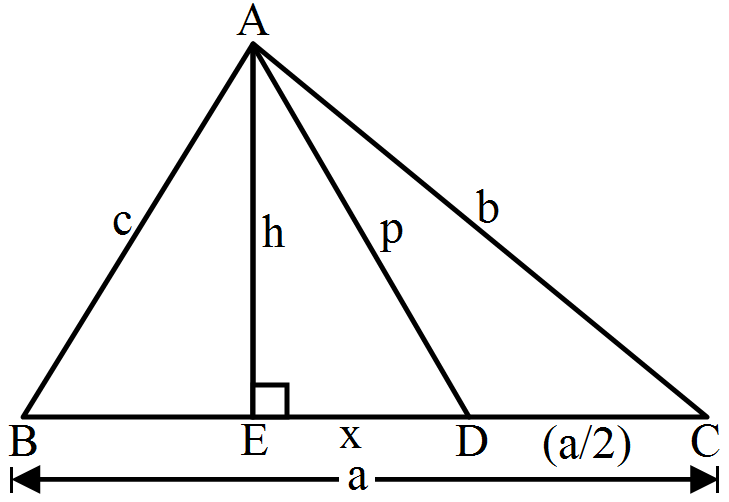
$(\text{b}^2-\text{c}^2)=2\text{ax}$ - 3View SolutionState the midpoint theorem.
- 4View SolutionThe sides of certain triangles are given below. Determine them are right triangles:
1.4cm, 4.8cm, 5cm. - 5View SolutionThe sides of certain triangles are given below. Determine them are right triangles:
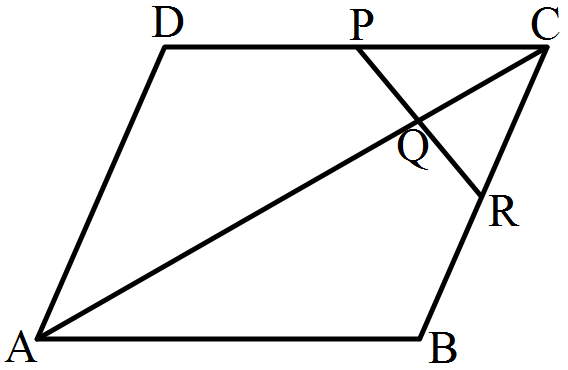
9cm, 16cm, 18cm. - 6ABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that $\text{CQ}=\frac{1}{4}\text{AC}.$ If PQ produced meets BC at R, prove that R is the midpoint of BC.View Solution
- 7The corresponding sides of two similar triangles ABC and DEF are BC = 9.1cm and EF = 6.5cm. If the rerimeter of $\triangle\text{DEF}$ is 25cm, find the perimeter of $\triangle\text{ABC}.$View Solution
- 8Find the length of altitude AD of an isosceles $\triangle\text{ABC}$ in which AB = AC = 2a units and BC = a units.View Solution
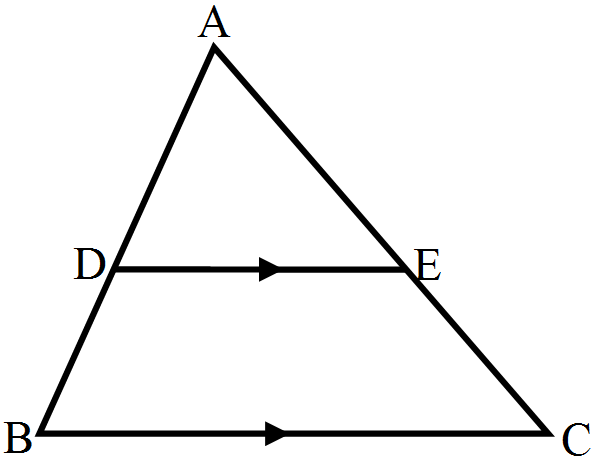
- 9D and E are points on the sides AB and AC respectively of a $\triangle\text{ABC}$ such that DE || BC: If $\frac{\text{AD}}{\text{AB}}=\frac{8}{15}$ and EC = 3.5cm, find AE.View Solution
- 10View SolutionFor the following statments state whether true (T) or false(F):
The ratio of the areas of two similar triangles is equal to the ratio of their corresponding angle-bisector segments.
