ધારો કે \(A\) અને \(B\) ગોળાઓ પર અનુક્રમે \(Q_1\) અને \(Q_2\) વિદ્યુતભાર જમા થાય છે અને તેમની ત્રિજ્યાઓ અનુક્રમે \(R_1\) અને \(R_2\) છે.
\(A\) ગોળાની સપાટી પર વિદ્યુત સ્થિતિમાન \(V_1 = kQ_1/ R_1 \)
\(B\) ગોળાની સપાટી પર વિદ્યુત સ્થિતિમાન \(V_2 = kQ_2/ R_2\)
જા \(V_1 > V_2\) હોય તો બંને ગોળાઓને તારથી જાડતાં \(A\) ગોળા પરથી વિદ્યુતભાર \(B\) ગોળા પર જશે.
ધારો કે \(A\) ગોળા પરથી \(q\) વિદ્યુતભાર \(B\) ગોળા પર જાય છે અને બંને ગોળાઓનું વિદ્યુતસ્થિતિમાન સમાન થશે.
\(\therefore \,\,{V_1}^\prime \, = \frac{{k({Q_1} - q)}}{{{R_1}}}\) અને \({V_2}^\prime \, = \frac{{k({Q_2} + q)}}{{{R_2}}}\)
\(\therefore \,\,{V_1}^\prime \, = {V_2}^\prime \,\,\,\,\therefore \,\frac{{{Q_1} - q}}{{{R_1}}}\, = \frac{{{Q_2} + q}}{{{R_2}}}\,\,\,\therefore \,\frac{{{Q_1} - q}}{{{Q_2} + q}} = \frac{{{R_1}}}{{{R_2}}}\,\,.....(i)\)
ગોળાઓની સપાટી પર વિદ્યુતક્ષેત્ર,
\({E_1} = \frac{{k({Q_1} - q)}}{{R_1^2}}\) અને \({{\text{E}}_{\text{2}}}\, = \frac{{k({Q_2} + q)}}{{R_2^2}}\,\,\,\therefore \,\frac{{{E_1}}}{{{E_2}}}\, = \left( {\frac{{{Q_1} - q}}{{{Q_2} - q}}} \right)\,\left( {\frac{{R_2^2}}{{R_1^2}}} \right)\, = \frac{{{R_1}}}{{{R_2}}}\, \times \left( {\frac{{R_2^2}}{{R_1^2}}} \right)\,\)
\( = \frac{{{R_2}}}{{{R_1}}}\, = \frac{{2mm}}{{1mm}}\,\,\,\therefore \,\frac{{{E_1}}}{{{E_2}}} = \frac{2}{1}\,\)(જો \({{\text{V}}_{\text{2}}}{\text{ > }}{{\text{V}}_{\text{1}}}\) લઈએ તો પણ આ જ પરિણામ મળે . )
Download our appand get started for free
Similar Questions
- 1ઇલેક્ટ્રોન તથા $\alpha$-કણને $100\, volt$ વિદ્યુત સ્થીતીમાનની અસર હેઠળ પ્રવેશીત કરવામાં આવે તો તેમના વેગમાનનો ગુણોત્તર....View Solution
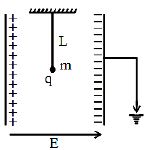
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે $L$ લંબાઈ ધરાવતા લોલકને $E$ વિદ્યુતક્ષેત્ર ધરાવતા સમાંતર પ્લેટ કેપેસીટર વચ્ચે મૂકેલું છે.તેનું દળ $m$ અને વિદ્યુતભાર $q$ હોય તો લોલકનો આવર્તકાળ કેટલો થશે?View Solution
- 3વોલ્ટેજ પ્રાપ્તિસ્થાન $V$ સાથે $n$ કેપેસિટરને સમાંતર જોડેલ છે.આ તંત્રમાં કેટલી ઊર્જાનો સંગ્રહ થાય?View Solution
- 4ઉગમબિંદુ પર એક બિંદુવત ડાયપોલ $\vec p = - {p_0}\hat x$ છે. ડાયપોલના કારણે $y-$ અક્ષ પર $d$ અંતરે વિદ્યુતસ્થિતિમાન અને વિદ્યુતક્ષેત્ર અનુક્રમે કેટલું થશે?(અનંત અંતરે $V = 0$)View Solution
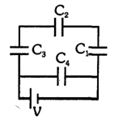
- 5$C_1 =1\ C, C_2 = 2\ C, C_3 = 3 \ C$ અને $C_4 = 4\ C$ ને સમાન કેપેસિટન્સ ધરાવતા ચાર કેપેસિટરોના નેટવર્કને આકૃતિ મુજબ, બેટરી સાથે જોડવામાં આવે છે. તો $C_2$ અને $C_4$ પરના વિદ્યુત ભારોનો ગુણોત્તર શોધો.View Solution
- 6ચિકિત્સામાં ઉપયોગમાં આવતા ડિફિબ્રીલેટર માટે લીધેલ $40\;\mu F$ ના કેપેસીટરને $3000\,V$ વડે ચાર્જ કરવામાં આવે છે. તેમાં સંગ્રહ પામતી ઉર્જા દરેક $2\,ms$ ના અંતરાલમાં દર્દીને આપવામાં આવે છે. તો દર્દીને અપાતો પાવર ......$kW$ હશે.View Solution
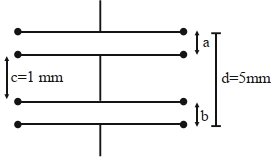
- 7આકૃતિમાં બતાવ્યા પ્રમાણે, $200\,cm ^2$ સમાન પ્લેટનું ક્ષેત્રફળ ધરાવતા બે સમાંતર પ્લેટ કેપેસિટરને એવી રીતે જોડાયેલા છે કે $a \neq b$. સંયોજનનું સમતુલ્ય કેપેસીટન્સ $x \varepsilon_0 F$ છે. $x$ ની કિંમત ................ છે.View Solution
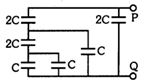
- 8આકૃતિમાં બતાવેલા સંયોજનમાં બિંદુ $P$ અને $Q$ વચ્ચે સમતુલ્ય કેપેસિટન્સનુંં મૂલ્ય શોધો.View Solution
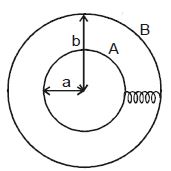
- 9$a$ અને $b\;(b > a)$ ત્રિજ્યાના ગોળીય વાહક $A$ અને $B$ હવામાં સમકેન્દ્રિત મૂકેલા છે. બંનેને કોપર તાર દ્વારા જોડવામાં આવે છે. તો તેમનો સમતુલ્ય કેપેસીટન્સ કેટલો થાય?View Solution
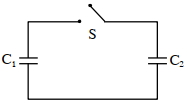
- 10બે સંઘારકો $C _{1}$ અને $C _{2}$ ને આકૃતિમાં દર્શાવ્યા અનુસાર જોડવામાં આવેલા છે. પ્રારંભમાં સંધારક $C _{1}$ ને $V$ વોલ્ટના સ્થિતિમાન તફવત થી બેટરી વડે વિદ્યુતભારિત કરવામાં આવે છે. હવે બેટરી દ્દૂર કરવામાં આવે છે અને આ રીતે વિદ્યુતભારિત $C_{1}$ સંધારકને કળ $S$ બંધ કરીને અવીજભારિત $C_{2}$ સંધારક સાથે જોડવામાં આવે છે. સંતુલન સ્થિતિ મેળવ્યા બાદ સંધારક $C _{2}$ પરનો વીજભાર ........ થશે.View Solution