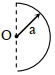
Considering symmetric elements each of length \(dl\) at \(A\) and \(B,\) we note that electric fields
perpendicular to \(PO\) are cancelled and those along \(PO\) are added. The electric field due to an
element of length \(dl\) ( \(a d \theta\) ) along \(PO\)
\(\mathrm{d} E=\frac{1}{4 \pi \mathcal{E}_{0}} \frac{\mathrm{d} q}{a^{2}} \cos \theta\)
\(=\frac{1}{4 \pi \mathcal{E}_{0}} \frac{\lambda \mathrm{d} l}{a^{2}} \cos \theta\)
\(=\frac{1}{4 \pi \mathcal{E}_{0}} \frac{\lambda(a \mathrm{d} \theta)}{a^{2}} \cos \theta\)
Net electric field at \(\mathrm{O}\)
\(E=\int_{-\pi / 2}^{\pi / 2} \mathrm{d} E=2 \int_{0}^{\pi / 2} \frac{1}{4 \pi \mathcal{E}_{0}} \frac{\lambda \cos \theta \mathrm{d} \theta}{a^{2}}\)
\(2 \cdot \frac{1}{4 \pi \mathcal{E}_{0}} \frac{\lambda}{a}[\sin \theta]_{0}^{\pi / 2}=2 \cdot \frac{1}{4 \pi \mathcal{E}_{0}} \cdot \frac{\lambda}{a} \cdot 1=\frac{\lambda}{2 \pi \mathcal{E}_{0} a}\)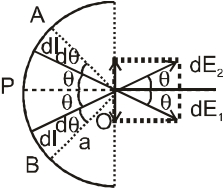
Download our appand get started for free
Similar Questions
- 1View Solutionઆકૃતિ વિદ્યુતક્ષેત્ર સાથે (સંલગ્ન) કેટલીક વિદ્યુત રેખાઓ દર્શાવે છે. તો......
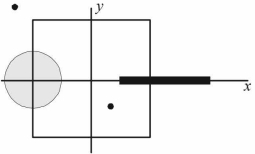
- 2$a/4$ ત્રિજ્યાની તકતી જે સમાન વિતરણ વિજભાર $6 c$ ધરાવે છે. તેને $x - y$ સમતલમા $(-a / 2,0,0)$ કેન્દ્ર સાથે તે માં મૂકવામાં આવે છે.$a$ લંબાઈનો સળિયો જે સમાન વિતરણ વીજભાર $8c$ ધરાવે છે તેને $X = a / 4$ થી $X =5 a / 4$ સુધી $X - axis$ પર મૂકેલ છે. જો બિંદુવત વીજભાર $-7 c$ અને $3 c$ ને $(a / 4,-a / 4,0)$ પર અને $(-3 a / 4,3 a / 4,0)$ પર મૂકેલ છે.બે સપાટી, $x=\pm a / 2, \quad Y =\pm a / 2, \quad Z =\pm a / 2$ દ્વારા બનતા ગોળાકાર સપાટીને ધ્યાનમાં લો. તેમાંથી પસાર થતું વિદ્યુત ફ્લક્સ $..........$View Solution
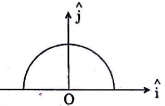
- 3એક પાતળી અને $r$ ત્રિજ્યાની અર્ધવર્તુળાકાર રીંગ ઉપર $q$ જેટલો ધન વિદ્યુતભાર સમાન રીતે પથરાયેલો છે. રીંગના કેન્દ્ર $O$ પર વિદ્યુતક્ષેત્રની તીવ્રતા $\overrightarrow{ E }$ કેટલી હશે?View Solution
- 4$\vec E\,\, = \,\,3\,\, \times \,\,{10^3}\,\hat i\,\,(N\,/\,\,C)$ લો. $10\, cm$ ની બાજુવાળા ચોરસમાંથી પસાર થતું ફલક્સ કેટલા .......$Nm^2/C$ હશે ? તેનો સ્પર્શક $X$ અક્ષ સાથે $60^°$ ખૂણો બનાવે છે.View Solution
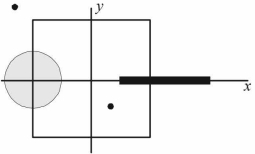
- 5$a/4$ ત્રિજ્યાની તકતી જે સમાન વિતરણ વિજભાર $6 c$ ધરાવે છે. તેને $x - y$ સમતલમા $(-a / 2,0,0)$ કેન્દ્ર સાથે તે માં મૂકવામાં આવે છે.$a$ લંબાઈનો સળિયો જે સમાન વિતરણ વીજભાર $8c$ ધરાવે છે તેને $X = a / 4$ થી $X =5 a / 4$ સુધી $X - axis$ પર મૂકેલ છે. જો બિંદુવત વીજભાર $-7 c$ અને $3 c$ ને $(a / 4,-a / 4,0)$ પર અને $(-3 a / 4,3 a / 4,0)$ પર મૂકેલ છે.બે સપાટી, $x=\pm a / 2, \quad Y =\pm a / 2, \quad Z =\pm a / 2$ દ્વારા બનતા ગોળાકાર સપાટીને ધ્યાનમાં લો. તેમાંથી પસાર થતું વિદ્યુત ફ્લક્સ $..........$View Solution
- 6સમઘનના કેન્દ્ર પર $Q\;\mu C$ વિદ્યુતભાર મૂકેલો છે. તો સમઘનના કોઈ પણ પૃષ્ઠમાંથી પસાર થતું ફ્લક્સ કેટલું હશે?View Solution
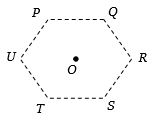
- 7સમાન મૂલ્યના ત્રણ ઘન અને ત્રણ ૠણ વિદ્યુતભારને ષટ્કોણના શિરોબિંદુ પર એવી રીતે મૂકવામાં આવે છે.જેથી કેન્દ્ર પર વિદ્યુતક્ષેત્ર એક ઘન વિદ્યુતભાર $R$ પર મૂકતાં ઉત્પન્ન થતાં વિદ્યુતક્ષેત્ર કરતાં બમણું હોય,તો નીચેનામાંથી $P,\,Q,\,R,\,S,\,T,\,$ અને $U$ પર મૂકવા પડતા વિદ્યુતભારોView Solution
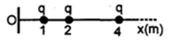
- 8View Solutionનીચે આપેલ આકૃતિમાં ઊગમબિંદુ આગળ અનંત સંખ્યાના વિદ્યુતભારને લીધે વિદ્યુતક્ષેત્રની ગણતરી કરો.
- 9આકૃતિમાં અનિયમિત વિધુતક્ષેત્ર $x-$ અક્ષની દિશામાં છે વિધુતક્ષેત્ર ધન $x-$ અક્ષ પર નિયમિત દરથી વધે છે વિધુતડાઈપોલને વિધુતક્ષેત્રમાં મૂકવામાં આવે છે તો નીચનામાંથી ક્યુ વિધાન સાચું થાય ?View Solution
- 10એક સમધનની કોઈ એક બાજુનાં મધ્યસ્થાન આગળ $q$ વિદ્યુતભાર મૂકવામાં આવેલ છે. સમધન સાથે સંકળાયેલ ફ્લકસ. . . . . . . . હશે.View Solution
