$\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9\,N m ^2\,C ^{-2}, g=10\,m s ^{-2}\right)$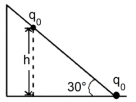
For equilibrium along the plane
\(mg \sin \theta=\frac{1}{4 \pi \epsilon_0} \times \frac{ q _0^2}{\left( h \operatorname{cosec} 30^{\circ}\right)^2}\)
\(\therefore h ^2=\frac{1}{4 \pi \epsilon_0} \times \frac{ q _0^2}{ mg \operatorname{cosec} 30^{\circ}}\)
\(=9 \times 10^9 \times \frac{\left(2 \times 10^{-6}\right)^2}{0.02 \times 10 \times 2}\)
\(\therefore h =3 \times 10^4 \times \frac{2 \times 10^{-6}}{0.2}\)
\(=0.3\,m\)
\(=300\,mm\)
Download our appand get started for free
Similar Questions
- 1અમુક અંતરે રહેલ ઈલેક્ટ્રોન અને પ્રોટોન વચ્ચેના કુલંબીય સ્થિતવિદ્યુત બળ અને ગુરુત્વાકર્ષણ બળનો ગુણોત્તર $2.4 \times 10^{39}$ છે. સમપ્રમાણ અચળાંક $K=\frac{1}{4 \pi \varepsilon_0}$ અને ગુરુત્વાકર્ષણ અચળાંક $G$ નો ગુણોત્તર લગભગ કેટલો હશે?View Solution
(આપેલ : પ્રોટોન અને ઇલેક્ટ્રોન દરેકનો વિદ્યુતભાર $=1.6 \times 10^{-19}\; C$, ઇલેક્ટ્રોનનું દળ $=9.11 \times 10^{-31}\; kg$, પ્રોટોનનું દળ $=1.67 \times 10^{-27}\,kg$)
- 2બે પાતળી વિધુતભારિત સમતલ સપાટીની $\sigma_{+}$ પુષ્ઠ ધનતા અને $\sigma_{-}$ છે. જયા $\left|\sigma_{+}\right|>\left|\sigma_{-}\right|$ બંને સમતલ લંબ છેદે છે. તો તંત્રની વિધુતક્ષેત્ર રેખાનું નિરૂપણView Solution
- 3આપેલ વિસ્તારમાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{i}+\frac{4}{5} E _{0} \hat{j}\right) \frac{ N }{ C }$ વડે આપવામાં આવે છે. $(y-z$ સમતલને સમાંતર) $0.2 \,m^ 2$ ક્ષેત્રફળ ધરાવતી અને $(x-y$ સમતલને સમાંતર) $0.3 \,m^2$ ક્ષેત્રફળ ધરાવતી લંબચોરસ સપાટીમાંથી બતાવેલ ક્ષેત્ર પસાર થતાં મળતા ફ્લક્સનો ગુણોત્તર $a:b$ છે, જ્યાં $a=...........$ છે.View Solution
[ અત્રે $\hat{i}, \hat{j}$ અને $\hat{k}$ એ અનુક્રમે $x, y$ અને $z-$ અક્ષોની દિશામાં એકમ સદિશ છે.]
- 4$R$ ત્રિજયાના ગોળા પર $2Q$ જેટલો કુલ વિદ્યુતભાર છે જેની વિદ્યુતભાર ઘનતા $\rho(r) = kr$ જ્યાં $r$ એ કેન્દ્રથી અંતર છે. બે વિદ્યુતભાર $A$અને $B$ જેનો વિદ્યુતભાર $-Q$ છે તેને ગોળાના વ્યાસ પર કેન્દ્ર થી સમાન અંતર પર છે. જો $A$ અને $B$ પર કોઈ બળ લાગતું ના હોય તો.....View Solution
- 5$1\, g$ જેટલા સમાન દળના બે સમાન ગોળાઓ પરનો સમાન વિદ્યુતભાર $10^{-9}\, C$ છે. જેમને સમાન લંબાઈની દોરીઓ વડે મુક્ત કરવામાં આવે છે. જો ગોળાનો કેન્દ્રો વચ્ચેનું અંતર $0.3\, cm$ હોય તો દોરીના પ્રક્ષેપણ કોણ શિરોલંબ ઘટક સાથે ...... હશે.View Solution
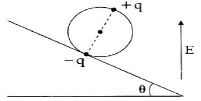
- 6$m $ દળના એક પૈડા પર વ્યાસના બે વિરુધ્ધ બિંદુઓ પર $+q$ અને $ -q$ વિદ્યુતભાર છે. એક ખરબચડા ઢળતા પાટિયા પર શિરોલંબ વિદ્યુતક્ષેત્ર $E$ ની હાજરીમાં તે સંતુલનમાં રહે છે. તો $E$ નું મૂલ્યView Solution
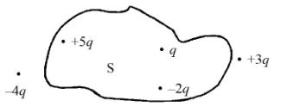
- 7પાંચ વિદ્યુતભારો $+q,+5 q,-2 q,+3 q$ અને $-4 q$ ને આક્રૂત્તિમાં દર્શાવ્યા અનુસાર ગોઠવવામાં આવ્યા છે.View Solution
સપાટી $s$ માંથી પસાર થતું આ વિદ્યુતભારોની ગોઠવણીને કારણે સંકળાયેલ ફ્લક્સ...........છે.
- 8$9.0\, cm$ ની ધારવાળા એક ઘનાકાર ગોસિયન સપાટીના કેન્દ્ર પર $2.0\; \mu \,C$ વિદ્યુતભાર રહેલો છે. આ સપાટીમાંથી કુલ વિદ્યુત ફલક્સ કેટલું હશે?View Solution
- 9વિદ્યુતભાર એ ઈલેક્ટ્રોનીક્સ ભાર $e$ નો પૂર્ણ ગુણાંક છે ઉપરનું વિધાન કોને સાબિત કર્યું છે?View Solution
- 10સમઘનના ખૂણા પર $Q$ વિદ્યુતભાર મૂકતાં સમઘનની એક બાજુમાંથી કેટલું ફલ્કસ પસાર થાય?View Solution