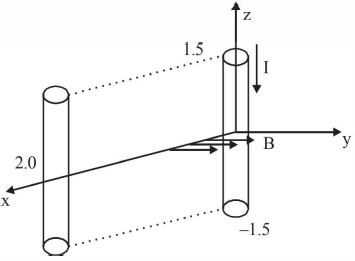
આકૃતિમાં બતાવ્યા પ્રમાણે એક સુવાહક કે જે $Z-$ અક્ષને સમાંતર $-1.5$$ \le Z < 1.5\,m$ વચ્ચે રહેલ છે,જેમાંથી $ - {\hat a_z}$ દિશામાં $10.0$ $A$ નો અચળ પ્રવાહ વહે છે.આપેલ સૂત્ર $\vec B$ $=$ $3.0 \times 10^{-4}$ $e^{-0.2x}$ ${\hat a_y}\,T$ માટે સુવાહકને અચળ ઝડપે $5 \times 10^{-3} $ $ s$ સમય ગાળામાં $x=2.0$ $m$ $,y=0$ $m$ સ્થાને લઇ જવા જરૂરી કાર્ય-દર .......$W$ માં શોધો.આ ગતિ $X-$ અક્ષને સમાંતર છે,એવું ધારો.

JEE MAIN 2014, Diffcult
a
Work done in moving the conductor is,
Work done in moving the conductor is,
\(W=\int_{0}^{2} F d x\)
\(=\int_{0}^{2} 3.0 \times 10^{-4} e^{-0.2 x} \times 10 \times 3 d x\)
\(=9 \times 10^{-3} \int_{0}^{2} e^{-0.2 x} d x\)
\(=\frac{9 \times 10^{-3}}{0.2}\left[-e^{-0.2 \times 2}+1\right] B=3.0 \times 10^{-4} e^{-0.2 x}\)
(By exponential function)
\(=\frac{9 \times 10^{-3}}{0.2} \times\left[1-e^{-0.4}\right]\)
\(=9 \times 10^{-3} \times(0.33)=2.97 \times 10^{-3}\, \mathrm{J}\)
Power required to move the conductor is, \(P=\frac{W}{t}\)
\(P=\frac{2.97 \times 10^{-3}}{(0.2) \times 5 \times 10^{-3}}=2.97 \,\mathrm{W}\)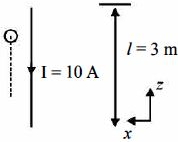
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સુરેખ તારમાંથી $ I$ પ્રવાહ પસાર થાય છે.તેમાંથી એક આંટાવાળી રીંગ બનાવતા કેન્દ્ર પાસે ચુંબકીયક્ષેત્ર $B$ છે.જો તેમાંથી ત્રણ આંટાવાળી રીંગ બનાવતા કેન્દ્ર પાસે ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 2View Solutionઓહમના નિયમમાં એમિટર અને વૉલ્ટમીટર ને અવરોધ શ્રેણી અથવા સમાંતરમાં જોડવામાં આવે છે.
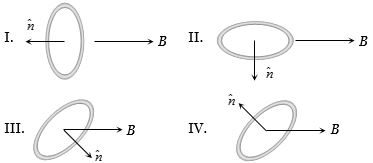
- 3$I, II, III,IV.$ લૂપની સ્થિતિઊર્જા ઘટતા ક્રમમાં નીચે પૈકી કઈ છે?View Solution
- 4એક પ્રોટોન ચુંબકીય ક્ષેત્રમાં લંબરૂપે વેગ $v$ સાથે દાખલ થાય છે, તો ભ્રમણનો આવર્તકાળ $T$ છે. જો પ્રોટોન $2 v$ વેગ સાથે દાખલ થાય, તો આવર્તકાળ કેટલો હશે?View Solution
- 5એક લાંબા સોલેનોઈડમાં $200$ આંટાઓ પ્રતિ $cm$ છે તથા પ્રવાહ $i$ છે. તેનાં મધ્યબિંદુ આગળ ચુંબકીયક્ષેત્ર $6.28 \times 10^{-2}\; Weber / m ^{2}$ છે. બીજા એક લાંબો સોલેનોઈડ $100$ આંટાઓ પ્રતિ $cm$ અને $\frac i3$ જેટલો પ્રવાહ ધરાવે છે. તો તેના મધ્યબિંદુ આગળ ચુંબકીયક્ષેત્ર કેટલું હશે?View Solution
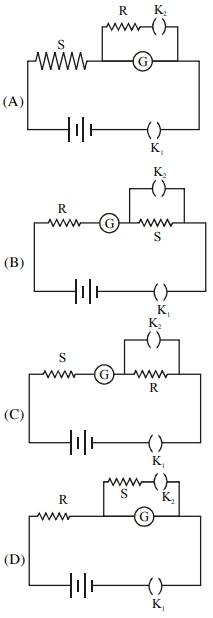
- 6આપેલ પરિપથ $(A, B, C$ અને $D$) માં $R$ ઊંચો અવરોધ અને $S$ ગેલ્વેનોમીટરનો પ્રવાહ નિયંત્રિત કરવા અવરોધ $S$ જોડેલો છે.તો આપેલ પતિપથમાંથી અર્ધઆવર્તન રીત માટેનો પરિપથ કયો થશે અને તેના માટે ગેલ્વેનોમીટરનો અવરોધ કેટલો થશે?View Solution
- 7View Solutionઆપેલ પરિપથમાં કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?
- 8સમાન ગતિ ઊર્જા ધરાવતા એક પ્રોટોન, એક ડ્યુટેરોન અને એક $\alpha-$ કણ નિયમિત્ત ચુંબકીય ક્ષેત્ર ધરાવતા વિસ્તારમાં ચુંબકીય ક્ષેત્રને લંબ ગતિ કરે છે. તેમના વર્તુળાકાર ગતિપથની ત્રિજ્યાઓનો ગુણોત્તર અનુક્રમે.......હશેView Solution
- 9$5\,cm,12\,cm$ અને $13\,cm$ બાજુઓ ધરાવતી કાટકોણ ત્રિકોણાકારની એક આંટાની પ્રવાહલૂપ $2\,A$ નો પ્રવાહ ધારણ કરે છે. આ લૂપ $0.75\,T$ મૂલ્ચના સમાન ચુંબકીયક્ષેત્રમાં લૂપની $13\,cm$ વાળી બાજુની સમાંતર દિશામાં મૂકવામાં આવે છે. $5\,cm$ ની બાજુ પર ચુંબકીય બળનું મૂલ્ય $\frac{x}{130}\,N$ છે. તો $x$ નું મૂલ્ય $...........$ છે.View Solution
- 10સૂચિ $I$ અને સૂચિ $II$ને મેળવોઃView Solution
આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરોઃ

