સળિયાનો \(x\) લંબાઈનો સૂક્ષ્મ ઘટક કે જે આકૃતિમાં દર્શાવ્યા પ્રમાણે \(q\) બિંદુવત્ વિદ્યુતભારથી \(x\) અંતરે આવેલ છે. ઘટકને બિંદુવત્ વિદ્યુતભાર તરીકે લો.
\(q\) અને વિદ્યુતભાર ઘટક વચ્ચેનું બળ
\(dF\,\, = \,\,\frac{1}{{4\pi \,\,{ \in _0}}}\,\,\frac{{q\,dQ}}{{{x^2}}}\) પરંતુ \(dQ\,\, = \,\,(Q/L)dx\) તેથી \(dF\,\, = \,\,\frac{1}{{4\pi \,\,{ \in _0}}}\,\,\frac{{q\,Q\,dx}}{{L{x^2}}}\)
\(\therefore \,\,F\,\, = \,\,\frac{1}{{4\pi \,\,{ \in _0}}}\,\,\,\frac{{qQ}}{L}\,\,\int\limits_d^{(d\,\, + \,\,L)} {\,\,\,\frac{{dx}}{{{x^2}}}} \,\, = \,\,\frac{1}{{4\pi \,\,{ \in _0}}}\,\,\frac{{qQ}}{L}\,\,\left[ { - \frac{1}{x}} \right]_d^{(d\,\, + \,\,L)}\)
\( \Rightarrow \,\,F\,\, = \,\,\frac{1}{{4\pi \,\,{ \in _0}}}\,\,\frac{{qQ}}{L}\,\,\left[ {\frac{1}{d}\,\, - \,\,\frac{1}{{(d\,\, + \,\,L)}}} \right]\,\, = \,\,\frac{1}{{4\pi \,\,{ \in _0}}}\,\,\,\frac{{qQ}}{{d(d\, + \,\,L)}}\)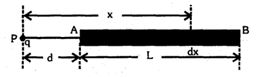
Download our appand get started for free
Similar Questions
- 1બે વિદ્યુત ડાયપોલની ડાયપોલ મોમેન્ટ $P$ અને $64 \,P$ છે.આ બંને ડાયપોલને વિરુધ્ધ દિશામાં $25 \,cm$ અંતરે મૂકેલા છે.તો $P$ ડાયપોલ મોમેન્ટવાળા ડાયપોલથી કેટલા......$cm$ ના અંતરે વિદ્યુતક્ષેત્ર શૂન્ય થાય?View Solution
- 2કોઈ વિભાગનું વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\frac{2}{5} E _{0} \hat{ i }+\frac{3}{5} E _{0} \hat{ j }$ છે, જ્યાં $E _{0}=4.0 \times 10^{3}\, \frac{ N }{ C }$ છે. $Y - Z$ સમતલમાં $0.4 \,m ^{2}$ ક્ષેત્રફળ ધરાવતી સપાટીનું વિદ્યુતફ્લક્સ ....... $Nm ^{2} C ^{-1}$ હશે.View Solution
- 3View Solutionમિલ્કનના તેલના ટીપાના પ્રયોગમાં, તેલના ટીપા પર નીચેના પૈકી કયો વિદ્યુતભાર હાજર હોય છે?
- 4ધારો કે એક નક્કર ગોળાની ત્રિજ્યા $R$ અને તેના પરનો વિદ્યુતભાર $Q$ છે. આ ગોળાનું વિદ્યુત ઘનતા વિતરણ $\rho( r )=\frac{ Q }{\pi R ^{4}} \cdot r$ સૂત્ર વડે અપાય છે. આ ગોળાની અંદર ગોળાના કેન્દ્રથી $r _{1}$ અંતરે આવેલા બિંદુ $P$ આગળ વિદ્યુતક્ષેત્રનું મૂલ્ય કેટલું થાય?View Solution
- 5જો એક બીજાથી $d$ અંતરે રહેલા બે વીજભારો $q_1$ અને $q_2$ ડાઈલેક્ટ્રીક અચળાંક $K$ ધરાવતા માધ્યમમાં રાખેલ છે. તો તેટલા સ્થિરવિદ્યુત બળ માટે હવાના માધ્યમમાં બે વીજભારો વચ્ચેનું સમતુલ્ય અંતર કેટલું હોય ?View Solution
- 6$L$ બાજુવાળા ષટકોણના પાંચ શિરોબિંદુ પર $+Q$ વિદ્યુતભાર મૂકેલા છે,તો કેન્દ્ર પર રહેલ $-Q$ વિદ્યુતભાર પર કેટલું બળ લાગે?View Solution
- 7$0.5\, m$ ત્રિજ્યાની અર્ધ વર્તૂળ રીંગ કુલ વિદ્યુતભાર $1.4 \times 10^{-9}\, C$ થી સમાન વિદ્યુતભારીત કરેલ છે. રીંગના કેન્દ્ર આગળ વિદ્યુતક્ષેત્રની તીવ્રતા ........$V/m$ છે.View Solution
- 8આપેલ વિસ્તારમાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\left(\frac{3}{5} E _{0} \hat{i}+\frac{4}{5} E _{0} \hat{j}\right) \frac{ N }{ C }$ વડે આપવામાં આવે છે. $(y-z$ સમતલને સમાંતર) $0.2 \,m^ 2$ ક્ષેત્રફળ ધરાવતી અને $(x-y$ સમતલને સમાંતર) $0.3 \,m^2$ ક્ષેત્રફળ ધરાવતી લંબચોરસ સપાટીમાંથી બતાવેલ ક્ષેત્ર પસાર થતાં મળતા ફ્લક્સનો ગુણોત્તર $a:b$ છે, જ્યાં $a=...........$ છે.View Solution
[ અત્રે $\hat{i}, \hat{j}$ અને $\hat{k}$ એ અનુક્રમે $x, y$ અને $z-$ અક્ષોની દિશામાં એકમ સદિશ છે.]
- 9View Solutionવિદ્યુત બળ રેખાઓની દિશામાં તેના વેગ સાથે ઈલેકટ્રોન તેના વિદ્યુતક્ષેત્રમાં દાખલ થાય તો.......
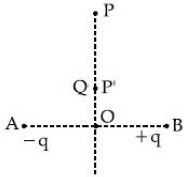
- 10વિધુતભારો $-q$ અને $+q$ એ અનુક્રમે $A$ અને $B$ પર સ્થિત છે જે વિદ્યુતદ્વિધ્રુવી રચે છે. અંતર $AB=2a$ અને $O$ એ આ દ્વિધ્રુવી $AB$ નું મધ્યબિંદુ છે. $OP$ એ આ દ્રિધુવી વિષુવ-રેખા અને $OP$ એ $AB$ લંબ છે. એક વિધુતભાર $Q$ ને $P$ પર મુકવામાં આવે છે, જ્યાં $OP=y$ અને $y > > 2a$. આ વિધુતભાર, $F$ જેટલું સ્થિત વિદ્યુત બળ અનુભવે છે. હવે જો $Q$ ને વિષુવરેખા પર $P$' કે જેથી $OP' = \frac{y}{3}$ સુધી ખસેડવામાં આવે તો $Q$ પરનું બળ ______ ની નજીકનું હશે. $\left( {\frac{y}{3} > > 2a} \right)$View Solution