આકૃતિમાં દર્શાવેલ ચોરસ તકતી $ABCD$ માટે નીચેનામાંથી કયો વિકલ્પ સાચો છે?
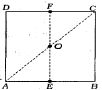

AIEEE 2007, Medium
d
By the theorem of perpendicular axes,
By the theorem of perpendicular axes,
\({I_z} = {I_x} + {I_y}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,or,\,\,{I_z} = 2{I_y}\)
\(\begin{array}{l}
\left( {\,{I_x} = {I_y}\,by\,symmetry\,of\,the\,figure} \right)\\
\therefore \,{I_{EF}} = \frac{{{I_z}}}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)
\end{array}\)
Again, by the same theorem
\(\begin{array}{l}
{I_z} = {I_{AC}} + {I_{BD}} = 2{I_{AC}}\\
\left( {\therefore \,{I_{AC}} = {I_{BD}}\,by\,symmetry\,of\,the\,figure} \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\therefore \,{I_{AC}} = \frac{{{I_z}}}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {ii} \right)
\end{array}\)
From \((i)\) and \((ii)\), we get \({I_{EF}} = {I_{AC}}\)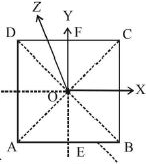
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionગતિ કરતાં વાહનોના પૈડા મધ્યમમાંથી પોલા અને પરીઘ પરથી જાડા હોય છે કારણ કે.....
- 2એક હળવી દોરીને $5\,kg$ દળ અને $70\,cm$ ત્રિજ્યા ધરાવતા એક પોલા નળાકારની આસપાસ વીટાળવામાં આવે છે. દોરીને $52.5\,N$ બળ વડે ખેંચવામાં આવે છે. નળાકારનો કોણીય પ્રવેગ .......... $rad\,s ^{-2}$ હશે.View Solution
- 3View Solutionકેન્દ્રીય બળની અસર હેઠળ કોનું સંરક્ષણ થાય?
- 4જો $\mathop {\rm{F}}\limits^ \to \, = \left( {\,4\hat i- 10\hat j\,} \right)$ અને $\mathop r\limits^ \to = \left( {\,5\hat i- 3\hat j\,} \right)$ હોય તો $\left( {\,\mathop \tau \limits^ \to = \mathop r\limits^ \to \times \mathop F\limits^ \to } \right)$ ની ગણતરી ... થાયView Solution
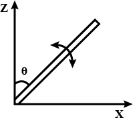
- 5$M$ દળના અને $l$ લંબાઈના એક સ્લેન્ડર એકસમાન સળીયાને એક છેડાથી ધરીમાં એ રીતે જોડેલ છે કે જેથી તે ઊર્ધ્વતલમાં ભ્રમણ કરી શકે (આકૃતિ જુઓ). ધરી પર અવગણ્ય ધર્ષણ છે. મુક્ત છેડાને ઊર્ધ્વ દિશામાં ધરીની ઉપરની તરફ રાખેલ છે અને ત્યારબાદ તેને મુક્ત કરવામાં આવે છે. સળિયાનો કોણીય પ્રવેગ જ્યારે તે ઊર્ધ્વ સાથે $\theta$ ખુણો બનાવે ત્યારે કેટલો હશે?View Solution
- 6$L$ લંબાઈ ધરાવતા અરેખીય ઘનતા ધરાવતા સળિયાની ઘનતા $\rho(\mathrm{x})={a}+{b}\left(\frac{\mathrm{x}}{\mathrm{L}}\right)^{2}$ મુજબ આપવામાં આવે છે જ્યાં $a$ અને $ {b}$ અચળાંક અને $0 \leq \mathrm{x} \leq \mathrm{L}$ છે.સળિયાના દ્રવ્યમાન કેન્દ્ર માટે $x$ નું મૂલ્ય કેટલું હોવું જોઈએ?View Solution
- 7$X$ અને $Z $ અક્ષ તકતીના સમતલમાં પરસ્પર લંબ છે અને $Y$ અક્ષ તકતીના સમતલને લંબ છે. જો પદાર્થની $X$ અને $Y$ અક્ષ પર જડત્વની ચાકમાત્રા અનુક્રમે $ 30\ kg m^2 $ અને $40\ kg m^2$ ત્યારે $Z$ અક્ષ પર જડત્વની ચાકમાત્રા ....... $kgm^2$ થશે .View Solution
- 8એક કણએ $(0,8)$ બિંદુુથી શરૂ થાય છે અને $\vec{v}=3 \hat{i} \,m / s$ ના નિયમિત વેગ સાથે ગતિ કરે છે. તો $5 \,s$ પછી ઊગમબિંદુ અનુલક્ષીને કણનો કોણીય વેગમાન .......... $kg m ^2 / s$ હશે. (કણ નું દળ $1 \,kg$ છે)View Solution
- 9ત્રણ સમાન પાતળી લાકડી જેની લંબાઈ $l$ અને દળ $M$ છે તેને જોડીને $H$ અક્ષર બનાવવામાં આવે તો તંત્ર ની $H $ ની કોઈ એક બાજુને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે ઍક ઘન ગોળો અને એક નળાકાર એક ઢાળ તરફ સમાન વેગથી સરક્યાં વગર ગતિ કરે છે.બંનેએ ઢાળ પર પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ $h_{sph}$ અને $h_{cyl}$ હોય તો ઊંચાઈનો ગુણોત્તર $\frac{{{h_{sph}}}}{{{h_{cyl}}}}$ શું થાય?View Solution

