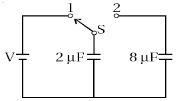
Initially, the energy stored in \(2\, \mu F\) capacitor is
\(U_{i}=\frac{1}{2} C V^{2}=\frac{1}{2}\left(2 \times 10^{-6}\right)\, V^{2}=V^{2} \times 10^{-6} \,\mathrm{J}\)
Initially, the charge stored in \(2 \,\mu \mathrm{F}\) capacitor is
\(Q_{i}=C V=\left(2 \times 10^{-6}\right) V=2 V \times 10^{-6}\) coulomb. When switch \(S\) is turned to position \(2,\) the charge flows and both the capacitors share charges till a common potential \(V_{c}\) is reached.
\(V_{C}=\frac{\text { total charge }}{\text { total capacitance }}=\frac{2 V \times 10^{-6}}{(2+8) \times 10^{-6}}=\frac{V}{5} \text { volt }\)
Finally, the energy stored in both the capacitors
\(U_{f}=\frac{1}{2}\left[(2+8) \times 10^{-6}\right]\left(\frac{V}{5}\right)^{2}=\frac{V^{2}}{5} \times 10^{-6}\, \mathrm{J}\)
\(\%\) loss of energy, \(\Delta U=\frac{U_{i}-U_{f}}{U_{i}} \times 100 \%\)
\(=\frac{\left(V^{2}-V^{2} / 5\right) \times 10^{-6}}{V^{2} \times 10^{-6}} \times 100 \%=80 \%\)
Download our appand get started for free
Similar Questions
- 1વોલ્ટેજ પ્રાપ્તિસ્થાન $V$ સાથે $n$ કેપેસિટરને સમાંતર જોડેલ છે.આ તંત્રમાં કેટલી ઊર્જાનો સંગ્રહ થાય?View Solution
- 2ત્રણ $4\,\mu F$ કેપેસીટન્સ ધરાવતા કેપેસીટરને એવી રીતે જોડવામાં આવે છે કે જેથી તેમનો સમતુલ્ય કેપેસીટન્સ $6\,\mu F$ મળે તો તેને કેવી રીતે ગોઠવેલા હશે?View Solution
- 3$1$ મી ત્રિજ્યા ધરાવતા ગોળાકાર વાહકનું કેપેસિટન્સ શું હશે ?View Solution
- 4$1\,mC$ વિદ્યુતભારથી $1\ metre$ અંતરે $2\,g$ દળ અને$1\,\mu \,C$ વિદ્યુતભાર ધરાવતો કણ મુકત કરતાં કણનો $10\ metres$ અંતરે વેગ કેટલા .......$m/s$ થાય?View Solution
- 5ઉગમબિંદુ પર એક બિંદુવત ડાયપોલ $\vec p = - {p_0}\hat x$ છે. ડાયપોલના કારણે $y-$ અક્ષ પર $d$ અંતરે વિદ્યુતસ્થિતિમાન અને વિદ્યુતક્ષેત્ર અનુક્રમે કેટલું થશે?(અનંત અંતરે $V = 0$)View Solution
- 6બે $q$ વિજભાર ધરાવતા બિંદુવત કણને છત સાથે નહિવત દળ ધરાવતી સમાન લંબાઇની દોરી સાથે જોડેલા છે. તે જ્યારે સમતોલનમાં આવે ત્યારે દોરી શિરોલંબ સાથે $\theta$ ખૂણો બનાવે છે.જો દરેક વિજભારિત કણનું દળ $m$ હોય તો તે બંનેને જોડતી રેખા પર વિદ્યુતસ્થિતિમાન કેટલો મળે?View Solution
$\left( {\frac{1}{{4\pi { \in _0}}} = k} \right).$
- 7$C$ જેટલુ કેપેસીટન્સ ધરાવતા $1000$ નાનાં ટીપાંઓ ભેગા થઈને જો એેક મોટું ટીપું બનાવે. તો બનતા નવા આકારો કેપેસીટન્સ કેટલો થશે ?View Solution
- 8ચાર્જ કરેલ કેપેસિટરની વચ્ચે વિદ્યુતભાર મૂકતાં તેના પર લાગતું બળ $F$ છે.હવે,એક પ્લેટને દૂર કરવાથી તેના પર કેટલું બળ લાગે?View Solution
- 9View Solutionપુરો વિદ્યુતભાર થયેલા એક સમાંતર પ્લેટવાળા કેેેસીટરને બેટરી સાથે જોડેલ રાખીને અવાહક સાધનો વડે તેની પ્લેટોને એકબીજાથી દૂર કરવામાં આવે છે. આ સ્થિતિમાં નીચેનામાંથી કઈ રાશિનું મૂલ્ય ઘટશે?
- 10$a$ અને $b$ ત્રિજયાની ગોળીય કવચથી કેપેસિટર બનાવવામાં આવે છે.બંને કવચ વચ્ચેનું માધ્યમ હવા છે.બહારની ગોળીય કવચ અને અંદરની ગોળીય કવચ વારાફરતી ગ્રાઉન્ડ કરવાથી બનતા કેપેસિટન્સ નો તફાવત કેટલો થાય? $(b>a)$View Solution
