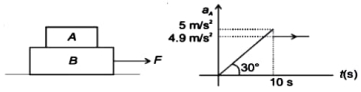
આકૃતિમાં દર્શાવ્યા મુજબ બ્લોક $A$ નો પ્રવેગ એ સમયની સાપેક્ષે બદલાય છે, તો બ્લોક $A$ અને $B$ નો ગતિક ઘર્ષણાંકનું મુલ્ય ..... છે.

Medium
a
(a)
(a)
Given: acceleration of block \(A\) varies with time as shown in figure To find the value of coefficient of kinetic friction between the block \(A\) and \(B\) Solution:
Force is applied on block \(B\). The moment when the block \(A\) starts sliding is the moment when the applied force \(F\) is greater than the frictional force between the two blocks.
Apply Newton's Second law of motion we get
\(\operatorname{ma}_i=\mu g m\)
\(\Rightarrow a _{\Lambda}=\mu g\)
\(\Rightarrow 4.9=\mu(9.8)\)
\(\Rightarrow \mu=0.5\)
is the value of coefficient of kinetic friction between the block \(A\) and \(B\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$400\,ms ^{-1}$ ની સમક્ષિતિજ ઝડપથી ગતિ કરતી $0.1\,kg$ દળની એક બુલેટ (ગોળી) ખરબચડી સમક્ષિતિજ સપાટી પર રાખેલ $3.9\,kg$ દળના બ્લોક સાથે અથડાય છે. બુલેટ આ બ્લોકમાં સ્થિર થઈ અને સંયુક્ત તંત્ર સ્થિર થાય તે પહેલા $20\,m$ અંતર કાપે છે.બ્લોક અને સપાટી વચ્ચેનો ધર્ષણાંક $......$ છે. (આપેલ $g =10\,m / s ^2$ )View Solution
- 2$m$ દળવાળો યોરસ બ્લોક $30^{\circ}$ ને ખૂણે રહેલ સમતલ પરથી $g / 4$ જેટલા પ્રવેગથી સરકે છે. તો ગતિક ધર્ષણાંકનું મૂલ્યView Solution
- 3એક નિયમિત $6\, m$ લાંબી ચેઈનને ટેબલ ઉપર એવી રીતે મૂકેલ છે કે જેથી તેની લંબાઈનો અમુક ભાગ ટેબલની ધાર આગળ લબડતો રહે. આ તંત્ર વિરામ સ્થિતિમાં છે. જે ચેઈન અને ટબલની સપાટી વચ્ચે સ્થિત ઘર્ષણક $0.5$ જેટલો હોય તો ચેઈનનો .........$m$ જેટલો મહ્ત્તમ ભાગ ટેબલ પરથી લટકતો રહી શકે.View Solution
- 4આકૃતિ માં દર્શાવ્યા પ્રમાણે $m$ દળનો એક નાનો દડો $A$ સ્થાને થી $v_0$ ઝડપે શરૂ કરીને ઘર્ષણરહિત માર્ગ $AB$ પર ગતિ કરે છે. માર્ગ $BC$ ઘર્ષણાંક $\mu $ ધરાવે છે. દડો $L$ અંતર કાપીને $C$ પર સ્થિર થાય છે, તો $L$ કેટલું હશે?View Solution

- 5એક સમતલ રસ્તા ઉપર $75 \,m$ ની ત્રિજ્યા ધરાવતો વળાંક છે. સરક્યા સિવાય વળાંક લઈ શકે તેવી કારની મહત્તમ ઝડપ $30\; m / s$ છે. હવે જો વળાંકની ત્રિજ્યા $48 \;m$ કરવામાં આવે અને પૈડા અને રસ્તા વચ્યે ધર્ષણાંક બદલાતો ના હોય તો મહત્તમ શક્ય ઝડપ............ $m / s$ થશે.View Solution
- 6$2 \,kg $ ના દળનો બ્લોક $0.4$ ઘર્ષણાંક ઘરાવતી સપાટી પર પડેલ છે.જો તેના પર $2.5\, N$ નું બળ લગાવતાં ઘર્ષણબળ ........ $N$ થાય.View Solution

- 7રોલર કોસ્ટર એવી રીતે બનાવવામાં આવ્યું છે, કે જયારે કાર તેની મહત્તમ ઊંચાઇએ જાય ત્યારે તેમાં બેઠેલી વ્યકિત વજનવિહીનતાનો અનુભવ કરે, રોલર કોસ્ટરની વક્રતાત્રિજયા $ 20\; m$ છે. સૌથી ઉપર ટોચ પર કારની ઝડપ ............. ની વચ્ચે હશે.View Solution
- 8$5 \,kg$ દળનો એક બ્લોક એે ખરબચડી ઢોળાવવાળી સપાટી પર સ્થિર છે. જો સમતલનો ખૂણો $60^{\circ}$ છે, તો તેના દ્વારા બ્લોક પર લગાડવામાં આવતું બળ ..... $N$ છેView Solution
- 9જ્યારે એક સિક્કાને ભ્રમણ કરતા ટેબલ પર તેના કેન્દ્રથી $1\,cm$ અંતરે મૂકવામાં આવે છે ત્યારે જ તે સરકવાનું શરૂ કરે છે. જો ભ્રમણ કરતા ટેબલનો કોણીય વેગ અડધો કરવામાં આવે, તો ........ $cm$ તે અંતરે રાખતા સરકશે.View Solution
- 10જો કોઈ બ્લોક $5 \,m / s$.ના વેગ સાથે $30^{\circ}$ ઢોળાવવાળી સપાટી ૫ર ઊધ્વદિશામાં ગતિ કરે છે, તે $0.5 \,s$ પછી અટકી જાય છે, તો પછી ઘર્ષણાંક લગભગ કેટલું હશે ?View Solution
