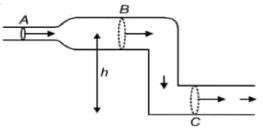
Solution by using Bernoulli's principle and equation of continuity Comparing points \(A\) and \(B\)

\(A_A V_A=A_B V_B\)   {equation of continuity} 

\(\because A_A < A_B\)

\(v_A > v_B\)

\(P_A+\frac{1}{2} \rho V_A^2+\rho g h=P_B+\frac{1}{2} \rho V_B^2+\rho g h\) {Bernoulli's equation}

\(\because v_A > v_B\)

\(\Rightarrow \frac{1}{2} \rho V_A^2 > \frac{1}{2} \rho V_B^2\)

\(\therefore P_A < P_B \quad \ldots (1)\)

Now comparing \(C\) and \(B\)

\(A_B=A_C \Rightarrow v_B=v_C\)

[equation of continuity].

\(P_B+\frac{1}{2} \rho V^2+\rho g h_B=P_C+\frac{1}{2} \rho V^2+\rho g h_C\)

\(\Rightarrow P_B+\rho g h_B=P_C+\rho g h_C\)

\(\because h_B > h_C \text { then } \quad \ldots (2)\)

\(P_B < P_C\)

Using \((1)\) and \((2)\)

We can say,  \(P_A  <  P_B  <  P_C\)