પાત્રમાં $ ‘h’ $ ઊંચાઇ સુધી પાણી ભરેલ છે.તળિયે નાનું છિદ્ર પાડવામાં આવે છે.પાણીની ઊંચાઇ $ h $ થી $\frac{h}{2}$ થતાં લાગતો સમય અને પાણીની ઊંચાઇ $\frac{h}{2}$ થી $ 0 $ થતા લાગતા સમયનો ગુણોત્તર કેટલો થાય?
Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$a $ ત્રિજયાની કેશનળી વચ્ચે દબાણનો તફાવત $P $ રાખવાથી પ્રવાહીનો વહન દર $Q$ છે.જો $ a/2 $ ત્રિજયા અને $2P $ દબાણ કરવાથી પ્રવાહીના વહન દર કેટલો થાય?View Solution
- 2$A$ ક્ષેત્રફળ ધરાવતા પાત્રમાં પાણી $3\,m$ ઊંચાઈ સુધી પાણી ભરેલ છે.તળીયેથી $52.5\, cm$ ઊંચાઈએ પાત્રની દીવાલમાં $‘A_0’$ ક્ષેત્રફળ ધરાવતું કાણું પાડવામાં આવે છે.જો $A_0/A = 0.1$ હોય તો $v^2$ ........ $m^2/s^2$ થાય. (જ્યાં $v$ એ કાણાંમાથી બહાર આવતા પાણીનો વેગ છે)View Solution
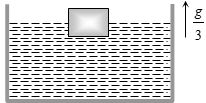
- 3સમઘન બ્લોકનું અડધું કદ ડુબેલું છે,પાત્રને $g/3$ પ્રવેગથી ઉપર તરફ ગતિ કરાવવાથી ડુબેલું નવું કદ કેટલું થાય?View Solution
- 4$900 Kg/m^3$ ઘનતા ધરાવતો બરફનો ટુકડો $1000 Kg/m^3 $ ઘનતા ધરાવતા પાણીમાં તરે છે,બરફનું ....... $\%$ કદ પાણીની બહાર રહે .View Solution
- 5$Viscosity$ એ પ્રવાહીનો એવો ગુણધર્મ છે જેથી $..............$View Solution
- 6$\sigma$ સાપેક્ષ ધનતા ધરાવતા એક ગોળાનો વ્યાસ $D$ છે અને તેને $d$ વ્યાસનો સમકેન્દ્રિય પોલાણ઼ (ખાડો) છે. જો તે ટેન્કમાંના પાણી પર તરી શકે તે માટે $\frac{\mathrm{D}}{\mathrm{d}}$ ગુણોત્તર ............ છે.View Solution
- 7$P$ દબાણનો તફાવત ધરાવતી નળીમાં પ્રવાહીનું વહન થાય છે.જો બમણી ત્રિજયા અને બમણી લંબાઇ ધરાવતી નળીમાં બમણા દરથી પ્રવાહીનું વહન કરવા માટે દબાણનો તફાવત કેટલો હોવો જોઈએ?View Solution
- 8$r$ ત્રિજ્યાં ધરાવતો એક નાનો ગોળો અવગણીય ધનતા ધરાવતા શ્યાન માધ્યમમાં પતન કરે ત્યારે 'V' જેટલો અંતિમ વેગ મેળવે છે. બીજો એક સમાન દળનો પરંતુ $2 r$ ત્રિજયા ધરાવતો નાનો ગોળો આ જ શ્યાન માધ્યમમાં પતન કરે તો તેનો અંતિમ વેગ...........View Solution
- 9બે નાના સમાન દળના અને $\rho_{1}$ અને $\rho_{2}\left(\rho_{1}=8 \rho_{2}\right)$ ઘનતા ધરાવતા ગોળાની ત્રિજ્યા અનુક્રમે $1\; mm$ અને $2\; mm$ છે. તે બંનેને એક $\eta$ શ્યાનતાગુણાંક વાળા અને $0.1{\rho}_{2} $ ઘનતા ધરાવતા પ્રવાહીમાં (સ્થિર સ્થિતિમાંથી) પાડવામાં આવે, તો તેમના ટર્મિનલ વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 10હવામાં સીસાા (લીડ) ગઠ્ઠાને વહન કરતી વખતે એક સ્પ્રિંગ બેલેન્સ $200 \,gF$ વાંચે છે. જો હવે સિસાને ખારા પાણીના દ્રાવણમાં તેના અડધા કદ જેટલું ડૂબાડવામાં આવે, તો સ્પિંગ બેલેન્સનું નવું વાંચન ......... $gF$ હશે ? સિસા (લીડ) અને ખારા પાણીનું વિશિષ્ટ ગુરુત્વ અનુક્રમે $11.4$ અને $1.1$ છે.View Solution