આકૃતિમાં દર્શાવ્યા પ્રમાણે એક પાતળા ચક્રની ત્રિજ્યા $R$ અને જડત્વની ચાકમાત્રા $I$ છે જે પોતાના દ્રવ્યમાન કેન્દ્રને અનુલક્ષીને મુક્ત રીતે ફરી શકે છે.તેના પર બે દળ $\mathrm{m}_{1}$ અને $\mathrm{m}_{2}\left(\mathrm{m}_{1}>\mathrm{m}_{2}\right)$ ને દળરહિત દોરી દ્વારા લટકવેળા છે.જ્યારે તંત્રને સ્થિર સ્થિતિમાંથી મુક્ત કરવામાં આવે ત્યારે $\mathrm{m}_{1}$ દળ નીચે તરફ $h$ અંતર સુધી ગતિ કરે ત્યારે ચક્રની કોણીય ઝડપ કેટલી થશે?
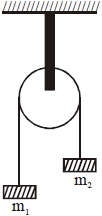

JEE MAIN 2020, Diffcult
b
by using work energy theorem
by using work energy theorem
\(\mathrm{Wg}=\Delta \mathrm{KE}\)
\(\left(\mathrm{m}_{1}-\mathrm{m}_{2}\right) \mathrm{gh}=\frac{1}{2}\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{V}^{2}+\frac{1}{2} \mathrm{I} \omega^{2}\)
\(\left(\mathrm{m}_{1}-\mathrm{m}_{2}\right) \mathrm{gh}=\frac{1}{2}\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right)(\omega \mathrm{R})^{2}+\frac{1}{2} \mathrm{I} \omega^{2}\)
\(\left(\mathrm{m}_{1}-\mathrm{m}_{2}\right) \mathrm{gh}=\frac{\omega^{2}}{2}\left[\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{R}^{2}+\mathrm{I}\right]\)
\(\omega=\sqrt{\frac{2\left(\mathrm{m}_{1}-\mathrm{m}_{2}\right) \mathrm{gh}}{\left(\mathrm{m}_{1}+\mathrm{m}_{2}\right) \mathrm{R}^{2}+\mathrm{I}}}\)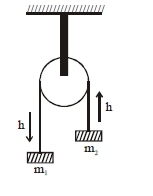
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપોલો અને ઘન ગોળાના દળ અને જડત્વની ચાકમાત્રા સમાન હોય,તો ત્રિજયાનો ગુણોત્તર કેટલો થાય?
- 2બે તક્તીઓ કે જે $1: 2$ ના ગુણોત્તરનું દળ ધરાવે છે અને $1: 8$ ગુણોત્તરની ત્રિજ્યા ધરાવે છે તે એક પછી એક $h$ ઊંચાઈના ઢોળાવવાળા સમતલ પરથી સરકયાં વગર નીચે ગબડે છે. જમીન પર પહોંચતાં તેમનાં રેખીય વેગનો ગુણોત્તર શોધો.View Solution
- 3એક રમતના મેદાનમાં એક ગોળ ફરતી તકતી જેનું વજન $120\ kg$ ત્રિજ્યા $4\ m$ અને ચક્રમાન ત્રિજ્યા $3\ m$ છે જ્યારે તકતી સ્થિર હોય ત્યારે એક $30\ kg$ દળનું બાળક $5\ m/sec$ ના વેગથી ટકટીના સ્પર્શકની દિશામાં તકતી પર ચડે છે જો ઘર્ષણને અવગણવામાં આવે તો બાળક અને ટકતીનો કોણીય વેગ ......... $ rad/sec$ થાય .View Solution
- 4$L $ લંબાઈનો પાતળા સળિયાને એક છેડેથી લટકાવેલો છે અને તે $ n $ ભ્રમણ પ્રતિ સેકન્ડથી ચાકગતિ કરે છે. સળિયાની ચાક ગતિ ઊર્જા કેટલી થશે ?View Solution
- 5$5\ kg$ દળ ધરાવતા સ્થિર પૈડા પર $30\ Nm $ જેટલું ટૉર્ક $15 $ સેકન્ડ માટે લગાડવામાં આવે છે. પૈડાની જડત્વની ચાકમાત્રા $2\ kg\ m^2$ છે. આ $10$ સેકન્ડમાં પૈડાએ કરેલું કોણીય સ્થાનાંતર ....... $\ rad$View Solution
- 6આકૃતિમાં દર્શાવ્યા પ્રમાણે ઍક ઘન ગોળો અને એક નળાકાર એક ઢાળ તરફ સમાન વેગથી સરક્યાં વગર ગતિ કરે છે.બંનેએ ઢાળ પર પ્રાપ્ત કરેલી મહત્તમ ઊંચાઈ $h_{sph}$ અને $h_{cyl}$ હોય તો ઊંચાઈનો ગુણોત્તર $\frac{{{h_{sph}}}}{{{h_{cyl}}}}$ શું થાય?View Solution

- 7એક $m$ દળ વાળા બોલને ઊર્ધ્વદિશામાં ફેકવામાં આવે છે અને તેજ દળના એક બીજા બોલને અધોદિશામાં ફેકવામાં આવે છે જેથી કરીને ગુરુત્વાકર્ષણ હેઠળ મુક્ત પણો ગતિ કરી શકે. દ્રવ્યમાન કેન્દ્રનો પ્રવેગ શોધો.View Solution
- 8$L$ લંબાઈ અને $M$ દળની લાકડી ઘર્ષણ રહિત સપાટી પર કોઇ પણ રીતે મુક્ત પણે ગતિ કરી શકે છે. $ m$ દળનો બોલ $ v$ ઝડપથી આકૃતિમાં દર્શાવ્યા પ્રમાણે ગતિ કરે છે. બોલનું દળ કેટલું હોવું જોઈએ કે જેથી અથડામણ બાદ તે સ્થિર રહે ?View Solution
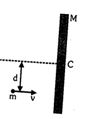
- 9એક પાતળી પણ દઢ અર્ધવતુળ વાયરની ફેમ જેની ત્રિજ્યા $r$ છે તેને $O$ આગળ લટકાવેલ છે અને તે પોતાના જ લંબગત સમતલ પર ફરે છે. એક હળવા $Peg$ $P$ ને $O$ થી શરૂ કરી અચળ વેગ $v _0$ થી આડી દિશામાં ગતિ કરે છે, અને ફ્રેમને ઊંચે લઈ જવાય છે. જ્યારે તે લંબ જોડે $60^{\circ}$ નો ખૂણો બનાવે ત્યારે આ ફ્રેમનો કોણીય વેગ શોધો.View Solution
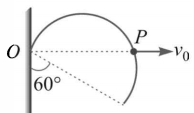
- 10View Solutionસમાન દળ અને ત્રિજ્યાનો એક નક્કર નળાકાર અને એક નક્કર ગોળો એક ખરબચડા ઢોળાવ વાળા સમતલ ઉપર સરક્યાં વિના ગબડે છે. ઘર્ષણ નું બળ કેટલું થાય?
