એક $\theta $ કોણવાળા ઢાળ પરથી સરકયા સિવાય ગબડીને અને ગબડયા સિવાય સરકીને નીચે આવતાં ઘન ગોળા (દળ $m$ અને ત્રિજયા $ R$) ના પ્રવેગનો ગુણોત્તર કેટલો થાય?
AIPMT 2014, Medium
a
Acceleration of the solid sphere slipping down the incline without rolling is
Acceleration of the solid sphere slipping down the incline without rolling is
\({a_{slipping}} = g\sin \theta \,\,\,\,\,\,\,...\left( i \right)\)
Acceleration of the solid sphere rolling down the incline without slipping is
\({a_{rolling}} = \frac{{g\sin \theta }}{{1 + \frac{{{k^2}}}{{{R^2}}}}} = \frac{{g\sin \theta }}{{1 + \frac{2}{5}}}\)
\(\left( {For\,solid\,sphere,\frac{{{k^2}}}{{{R^2}}} = \frac{2}{5}} \right)\)
\(= \frac{5}{7}g\sin \theta \,\,\,\,\,...\left( {ii} \right)\)
Divide eqn. \((ii)\) by eqn. \((i)\), we get
\(\frac{{{a_{rolling}}}}{{{a_{slipping}}}} = \frac{5}{7}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
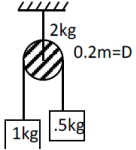
- 1આકૃતિમાં દર્શાવેલ $0.2\, m$ વ્યાસ અને $2\, kg$ દળ ધરાવતી પુલી પર રહેલ $1\, kg$ દળના પદાર્થનો પ્રવેગ ($m / s ^{2}$ માં) કેટલો હશે?View Solution
- 2View Solutionકઈ અક્ષ પર રિંગની જડત્વની ચાકમાત્રા મહત્તમ થશે ?
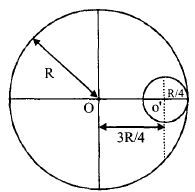
- 3આકૃતિમાં દર્શાવ્યા મુજબ $M$ દળ અને $R$ ત્રિજ્યાની એક પાતળી નિયમિત તકતીમાં $\frac{R}{4}$ ત્રિજ્યાનો વર્તુળાકાર છેદ પાડેલો છે. તો બાકી રહેલા ભાગ ની તેના $O$ માથી પસાર થતી અક્ષને અનુલક્ષીને તકતીના સમતલને લંબ જડત્વની ચાકમાત્રા શું થાય?View Solution
- 4જો એક ઘન ગોળો અને નળાકાર ની ત્રિજ્યા અને ઘનતા સમાન હોય તો તેની પોતાની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કોના માટે મહત્તમ હોય $(L=R )$ ?View Solution
- 5View Solutionએક પાતળી વર્તુળાકાર વીટી સૌપ્રથમ એક ઢોળાવયુક્ત સપાટી ઉપરથી નીચે સરકે છે અને ત્યાર બાદ તેજ ઊંચાઈથી સમાન ભૂમિતિના એક ખરબચડા ઢોળાવ ઉપરથી નીચે ગબડે છે. બે ગતિઓમાં લેવાયેલ સમયનો ગુણોત્તર શું થાય?
- 6જયારે પંખો ચાલુ કરવામાં આવે છે ત્યારે પ્રથમ $3\, sec$ માં $10 $ પરિભ્રમણ કરે છે. પછી બીજી $3\, sec$ માં કેટલા પરિભ્રમણ કરશે $?$ (અહીં અચળ કોણીય પ્રવેગ લાગે છે.)View Solution
- 7એક દડો સરકયા વિના ગબડે છે.દડાના દ્રવ્યમાન કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજયા $K$ છે.જો દડાની ત્રિજયા $R$ હોય, તો કુલઊર્જાનો કેટલામો ભાગ ચાકગતિ ઊર્જાના સ્વરૂપમાં હશે?View Solution
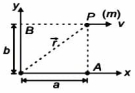
- 8એક કણ $x$ -અક્ષને સમાંતર સીધી રેખામાં અયળ વેગથી ગતિ કરી રહ્યો છે. સદિશ સ્વરૂપમાં ઊગમ બિંદુને અનુલક્ષીને કોણીય વેગમાન શોધો.View Solution
- 9View Solutionપાતળી મીટર પટ્ટીનો એક છેડો જમીન પર રહે તેમ ગોઠવેલી છે એક છેડાનો સંપર્ક સ્થાયી રહે તેમ નીચે પડવા દેવામાં આવે છે તો તેની સૌથી ઉપરના છેડો જમીનને અથડાય ત્યારે વેગ શોધો.
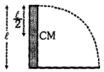
- 10કેન્દ્રમાંથી પસાર થતી અને લંબાઈને લંબરૂપે રહેલ અક્ષને અનુલક્ષીને એક નળાકારીય સળિયાની ચક્રાવર્તન ત્રિજ્યા $(radius\,of\,gyration) \dots \dots m$ હશે. (સળિયાની લંબાઈ $10 \sqrt{3} m$ આપેલ છે).View Solution
