આકૃતિમાં દર્શાવ્યા મુજબ $R$ અને $2 {R}$ ત્રિજ્યાના બે ગ્રહો (ગોળાકાર) જેમના દળ $M$ અને $9\, M$ છે જેનાં કેન્દ્રો વચ્ચેનું અંતર $8 \,R$ છે. $M$ દળના એક ઉપગ્રહને $M$ દળના ગ્રહની સપાટી પરથી બીજા ગ્રહના કેન્દ્ર તરફ ફેંકવામાં આવે છે. આ પદાર્થ બીજા ગોળાની સપાટી પર પહોંચે તે માટે જરૂરી લઘુતમ ઝડપ $\sqrt{\frac{a}{7} \frac{G M}{R}}$ હોય તો $a$ નું મૂલ્ય કેટલું હશે?
[આપેલ : બંને ગ્રહો પોતાના સ્થાને સ્થિર જકડી રાખેલ છે.]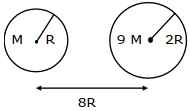
JEE MAIN 2021, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m$ દળ ધરાવતો પદાર્થ $M$ દળ આધારવતા ગ્રહની ફરતે $R$ ત્રિજ્યાવાળી કક્ષામાં ભ્રમણ કરે છે.કોઈ એક સમયે તે બે સમાન દળમાં વિભાજિત થાય છે.પ્રથમ દળ $\frac{R}{2}$ ત્રિજ્યાવાળી કક્ષામાં ભ્રમણ કરે છે અને બીજું દળ $\frac{3R}{2}$ ત્રિજ્યાવાળી કક્ષામાં ભ્રમણ કરે છે.તો શરૂઆતની અને અંતિમ કુલ ઉર્જાનો તફાવત કેટલો થાય?View Solution
- 2કોઈ સ્થાને ગુરુત્વાકર્ષણક્ષેત્ર $\vec E$ $=(5\,N / kg)\, \hat i + (12\,N / kg)\,\hat j$ મુજબ પ્રવર્તે છે.જો કેન્દ્ર આગળ સ્થિતિમાન શૂન્ય લેવામાં આવે તો $(12\,m, 0)$ અને $(0, 5\,m)$ અંતરે રહેલ સ્થિતિમાનનો ગુણોત્તર કેટલો થાય?View Solution
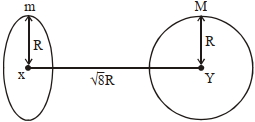
- 3આકૃતિમાં દર્શાવેલ ગોળા અને વલય (રીંગ) વચ્ચે આકર્ષણ બળ શોધો, જ્યાં રીંગનું સમતલ કેન્દ્રોને જોડતી રેખાને લંબરૂપે છે. બે રિંગ $('m'$ દળ) નાં કેન્દ્ર થી ગોળા $('M'$ દળ)નાં કેન્દ્ર વચ્ચેનું અંતર $\sqrt{8} R$ હોય તેમજ બંને એકસરખી ત્રિજ્યા $'R’$ ધરાવે છે.View Solution
- 4જો પૃથ્વીની ત્રિજ્યા $6000\, km$ હોય તો સપાટી થી $6000 \,km $ ઊંચાઈએ પદાર્થનું વજન તેના સપાટી પરના વજન કરતાં...View Solution
- 5પૃથ્વી પર પદાર્થ નું દળ $M$ હોય તો ચંદ્ર પર તેનું દળ કેટલું થાય?View Solution
- 6પૃથ્વીના કેન્દ્રથી $r$ અંતરે રહેલા $m$ દળના $A$ ઉપગ્રહ અને પૃથ્વીના કેન્દ્રથી $2r$ અંતરે રહેલા $2m$ દળના $B$ ઉપગ્રહના આવર્તકાળનો ગુણોત્તર કેટલો થાય?View Solution
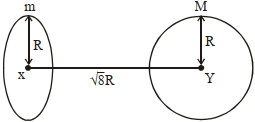
- 7આકૃતિમાં દર્શાવેલ ગોળા અને વલય (રીંગ) વચ્ચે આકર્ષણ બળ શોધો, જ્યાં રીંગનું સમતલ કેન્દ્રોને જોડતી રેખાને લંબરૂપે છે. બે રિંગ $('m'$ દળ) નાં કેન્દ્ર થી ગોળા $('M'$ દળ)નાં કેન્દ્ર વચ્ચેનું અંતર $\sqrt{8} R$ હોય તેમજ બંને એકસરખી ત્રિજ્યા $'R’$ ધરાવે છે.View Solution
- 8કોઇ ઉપગ્રહને $2R$ ત્રિજયાવાળી કક્ષામાંથી $3R$ ત્રિજયાવાળી કક્ષામાં લઇ જતાં તેની ઊર્જામાં કેટલો ફેરફાર થાય? ($R$= પૃથ્વીની ત્રિજયા)View Solution
- 9View Solutionમાણસની પૃથ્વીની વિષુવવૃત્ત થી ધ્રુવ તરફની ગતિ દરમિયાન તેનું વજન એ ..... ( પૃથ્વીની ત્રિજ્યામાં થતો ફેરફાર અવગણો )
- 10જો $M$ એ પૃથ્વીનું દળ અને $R$ એ પૃથ્વીની ત્રિજ્યા તો ગુરુત્વ પ્રવેગ અને ગુરુત્વાકર્ષણ નો અચળાંક નો ગુણોત્તર કેટલો થાય?View Solution