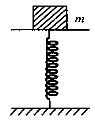
આકૃતિમાં દર્શાવ્યા મુજબ શિરોલંબ ગોઠવેલ સ્પ્રિંગ પર હલકા સપાટ પાટિયા પર $2\; kg$ દળનો પદાર્થ મૂકેલો છે. સ્પ્રિંગ અને પાટિયાનું દળ અવગણ્ય છે. સ્પ્રિંગને થોડી દબાવીને છોડી દેતાં તે સરળ આવર્ત ગતિ કરે છે. સ્પ્રિંગનો બળ અચળાંક $200\; N/m$ છે. આ દોલનનો ઓછામાં ઓછો કંપવિસ્તાર કેટલો હોવો જોઇએ જેથી પદાર્થ એ પાટિયા પરથી છૂટો પડી જાય? ($g=10 m/s^2$ લો)

AIPMT 2007, Medium
a
The spring has a length \(l .\) Whem \(m\) is placed over it, the equilibrium position becomes \(O^{\prime}\)
The spring has a length \(l .\) Whem \(m\) is placed over it, the equilibrium position becomes \(O^{\prime}\)
If it is pressed from \(O^{\prime}\) \((the\, equilibrium\, position)\) to \(O^{\prime \prime}, O^{\prime} O^{\prime \prime}\) is the amplitude.
\(O O^{\prime} =\frac{m g}{k}=\frac{2 \times 10}{200}=0.10 \mathrm{m} \)
\(m g =k x_{0}\)
If the restoring force \(m A \omega^{2}>m g,\) then the mass will move up with acceleration, detached from the pan.
i.e. \(A>\frac{g}{k / m} \Rightarrow A>\frac{20}{200}>0.10 \mathrm{m}\)
\(The\, amplitude >10 \mathrm{cm}\)
i.e. the minimum is just greater than \(10 \mathrm{cm}\). (The actual compression will include \(x_{0}\) also. But when talking of amplitude, it is always from the equilibrium position with respect to which the mass is oscillating.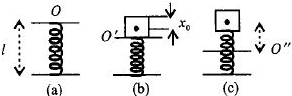
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સાદા લોલક કે જે સ.આ.ગ. કરે છે. તેની ગતિ નીચેના સમીકરણથી દર્શાવવામાં આવે છે.View Solution
$y=A \sin (\pi t+\phi)$
લોલકની લંબાઈ ..........$cm$
- 2દોરી વડે લટકાવેલ એક બોલ શિરોલંબ સમતલમાં એવી રીતે ગતિ કરે છે કે જેથી તેના અત્યંત બિંદુ અને સૌથી નીચેનાં બિંદૂ આગળ પ્રવેગનું મૂલ્ય સમાન રહે. અંત્ય બિંદુ આગળ માટે દોરીનાં આવર્તન કોણ $(\theta)$_____થશે.View Solution
- 3સરળ આવર્ત ગતિ કરતા કણનો કંપવિસ્તાર $a$ છે. તેનો આવર્તકાળ $T$ છે. આ કણને સમતોલન સ્થાનથી કંપવિસ્તારના અડધા મૂલ્ય સુધી જતાં કેટલો સમય લાગશે?View Solution
- 4$y(cm) = \sin \frac{\pi }{2}\left( {\frac{t}{2} + \frac{1}{3}} \right).$ સરળ આવર્તગતિ કરતા પદાર્થનો મહતમ પ્રવેગ કેટલો ..... $cm/sec^2$ થાય?View Solution
- 5ઉગમબિંદુને અનુલક્ષીને કણ $x-$અક્ષ પર દોલનો કરે છે. તેની સ્થિતિઉર્જા $V(x) = k | x |^3$ મુજબ બદલાય છે. જ્યાં $k$ ધન અચળાંક છે. જો તેનો કંપવિસ્તાર $a$ હોય તો તેનો આવર્તકાળ $T$....View Solution
- 6સાદા લોલકની લંબાઇમાં $2\% $ નો વધારો કરવામાં આવે છે. આવર્તકાળમાં થતો વધારો ........$\%$View Solution
- 7$10\ cm$. કંપવિસ્તારથી $5\ gm$ દળ સરળ આવર્તગતિ કરે છે.તેનો મહતમ વેગ $100\ cm/sec$.છે.તેનો વેગ $50\ cm/sec$ કયાં અંતરે થશે?View Solution
- 8View Solutionએક કણ નિયમિત ઝડપથી વર્તુળમાં ગતિ કરે છે. આ ગતિ .....
- 9$F = sin\,t\,N$ બાહ્યબળ લાગતાં સરળ આવર્ત દોલનો કરતાં પદાર્થની કોણીય આવૃતિ $2\,rad\,s^{-1}$ છે. જો $t = 0$ સમયે તે સમતોલન સ્થાને હોય તો પછીના સમયે તે કોના સમપ્રમાણમાં હશે?View Solution
- 10પુન: સ્થાપક બળ સ્થાનાંતરના સપ્રમાણમાં અને અવરોધક બળ વેગના સપ્રમાણમાં હોય તેવા કણ પર $Fsin\omega t$ બળ લાગે છે. જો કણનો કંપવિસ્તાર $\omega = {\omega _1}$ માટે મહત્તમ અને કણની ઊર્જા $\omega = {\omega _2}$ માટે મહત્તમ હોય, તો ........ (જ્યાં $\omega_0$ દોલન કરતાં કણની પ્રાકૃતિક આવૃતિ છે)View Solution
