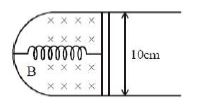
આકૃતિમાં દર્શાવ્યા પ્રમાણે $10\, cm$ લંબાઈ ધરાવતી પટ્ટી ને $U$ આકારમાં વાળીને તેને $0.5\,Nm^{-1}$ બળ અચળાંક ધરાવતી સ્પ્રિંગ સાથે જોડેલ છે.તંત્રને $0.1\, T$ ધરાવતા ચુંબકીય ક્ષેત્રમાં મુકેલ છે.જો પટ્ટીને સંતુલન અવસ્થામાથી ખેચવામાં આવે તો તો તેનો કંપવિસ્તાર $e$ માં ભાગનો થાય ત્યાં સુધી $N$ દોલનો કરે છે.જો પટ્ટીનું દળ $50\, grams$ ,અવરોધ $10\,\Omega $ અને હવાનો અવરોધ અવગણવામાં આવે તો $N$ કેટલો હશે?

JEE MAIN 2019, Diffcult
d
\(\mathrm{T}_{0}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}=\frac{2 \pi}{\sqrt{10}}\)
\(\mathrm{T}_{0}=2 \pi \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}=\frac{2 \pi}{\sqrt{10}}\)
\(\mathrm{A}=\mathrm{A}_{0} \mathrm{e}^{-1 / \gamma}\)
\(\therefore\) for \(\mathrm{A}=\frac{\mathrm{A}_{0}}{\mathrm{e}}, \mathrm{t}=\gamma\)
\(\mathrm{t}=\gamma=\frac{2 \mathrm{m}}{\mathrm{b}}=\frac{\frac{2 \mathrm{m}}{\mathrm{B}^{2} \ell^{2}}}{\frac{\mathrm{B}^{2} \ell^{2}}{\mathrm{R}}}=10^{4} \,\mathrm{s}\)
\(\therefore \) No of oscillation \(\frac{\mathrm{t}}{\mathrm{T}_{0}}=\frac{10^{4}}{2 \pi / \sqrt{10}} \approx 5000\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionટ્રાન્સફોર્મરના કોરમાં એડી પ્રવાહ કઇ રીતે ધટે?
- 2$10\, {mH}$ ના ઇન્ડક્ટરને $10\, {k}\, \Omega$ અવરોધ અને સ્વીચ દ્વારા $20\, {V}$ બેટરી સાથે જોડાયેલ છે. લાંબા સમય પછી, જ્યારે મહત્તમ પ્રવાહ પસાર થાય ત્યારે સ્વીચ બંધ થાય તેવી રીતે પરિપાટ તૈયાર કરેલ છે. $1\, \mu\, {s}$ પછી પરિપથમાં પ્રવાહ $\frac{{x}}{100}\, {mA}$ હોય, તો ${x}$ કોને બરાબર થાય?View Solution
(${e}^{-1}=0.37$ લો)
- 3${l_0}$ લંબાઇ અને $L$ ઇન્ડકટન્સ ધરાવતા સોલેનોઇડ બનાવવા માટે કેટલી લંબાઇના તારની જરૂર પડે?View Solution
- 4$L-R$ પરિપથમાં $R$ અવરોધ અને $L$ ઇન્ડકટન્સને બેટરી સાથે જોડતાં પ્રવાહમાં કેટલો વધારો થાય?View Solution
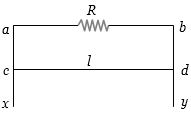
- 5$l$ લંબાઇ અને $m$ દળ ધરાવતા $cd$ તાર $ax$ અને $by$ ઘર્ષણરહિત પથ પર ગતિ કરે છે.આ પથ પર $a$ અને $b$ વચ્ચે $R$ અવરોધ છે. $abcd$ સમતલને લંબ અચળ ચુંબકીય ક્ષેત્ર $B$ લગાવેલ હોય તો $cd$ કેટલા અચળ વેગથી ગતિ કરશે?View Solution
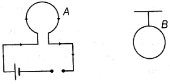
- 6તંત્રમાં બે કોઇલ $A$ અને $B$ છે. કોઇલ $A$ માં અચળ પ્રવાહ $I$ પસાર થાય છે.જ્યારે કોઇલ $B$ ને નજીકમાં મૂકેલી છે, હવે તંત્રને ગરમ કરવામાં આવે છે, તેથી બંન્ને કોઇલનું તાપમાન વધે તો,View Solution
- 7$80 cm^2 $ ક્ષેત્રફળ અને $50$ આંટા ધરાવતી તકતી $0.05Tesla$ ના ચુંબકીયક્ષેત્રમાં $2000 $ પરિભ્રમણ$/min$ થી ફરે છે,તો કેટલું $emf$ ઉત્પન્ન થાય?View Solution
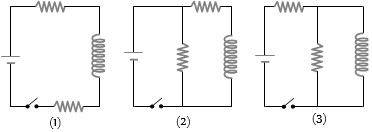
- 8બધા પરિપથમાં સમાન બેટરી,ઇન્ડકટર અને અવરોધ છે,બેટરીમાંથી પસાર થતો પ્રવાહ $(i)$ કળ બંધ કરતાં તરત જ $(ii)$ કળ બંધ કરતાં ઘણા સમય પછી , પ્રવાહ ઉતરતા ક્રમમાં નીચે પૈકી કયો થાય?View Solution
- 9View Solutionવિદ્યુતઊર્જાનું યાંત્રિક ઊર્જામાં રૂપાંતર કયું સાઘન કરે છે.
- 10$10^{-2} T$ ઘરાવતા ચુંબકીય ક્ષેત્રમાં 30cm ત્રિજયા,એક આંટા ઘરાવતું અને ${\pi ^2}$Ω અવરોઘ ઘરાવતું વર્તુળાકાર ગૂંચળું મૂકેલ છે.આ ગૂંચળું ચુંબકીયક્ષેત્રને લંબ તેમજ તેના વ્યાસને અનુલક્ષીને $200\, rpm$ ની ઝડપે ભ્રમણ કરે છે,તો ગૂંચળામાં ઉદ્ભવતા $AC$ પ્રેરિત પ્રવાહનું મૂલ્ય _______$mA $ હશે.View Solution
