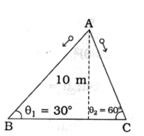
આકૃતિમાં દર્શાવ્યા પ્રમાણે બે ગોળાઓને બિંદુ $A$ થી અનુક્રમે $AB$ તથા $AC$ પથ પર મુક્ત કરવામાં આવે છે, તો બંને ગોળાને ઢાળના તળિયે પહોંચવા માટે લાગતા સમય અનુક્રમે.......અને.......થાય. બંને સપાટીઓ લીસી ($g = 10 m/s^2$ લો.)

Diffcult
a
ગોળો \(A \) અને \(B\) બંને સમાન ઊચાંઇએથી નીચે આવતા હોવાથી, બંને માટે સ્થિતિ- ઊર્જા \(mgh\) = ગતિ-ઊર્જા \(1/2 mv^2\)
ગોળો \(A \) અને \(B\) બંને સમાન ઊચાંઇએથી નીચે આવતા હોવાથી, બંને માટે સ્થિતિ- ઊર્જા \(mgh\) = ગતિ-ઊર્જા \(1/2 mv^2\)
\(\therefore \upsilon \, = \,\sqrt {2gh} \,\, = \,\sqrt {2 \times 10 \times 10} \,\,\, = \,\sqrt {200} \,\,\, = \,14.14\,\,m/s\)
હવે, ગોળો \(A\) ને જમીન પર પહોંચવા લાગતો સમય શોઘવા માટે \(\upsilon \, = \,{\upsilon _0}\, + \,g\,\sin \,{\theta _1}\, \cdot \,{t_1}\) પરંતુ \(v_0 = 0 \) છે.
\(\therefore \,{t_1}\, = \,\frac{\upsilon }{{g\,\sin \,{\theta _1}}}\,\,\, = \,\,\,\frac{{14.14}}{{10\,\sin \,{{30}^ \circ }}}\,\,\, = \,2\sqrt 2 \,\) સેકન્ડ
તેવી જ રીતે ગોળો \(B\) ને જમીન પર પહોંચવા લાગતો સમય શોઘવા માટે \(v = v_0 + g sin \theta_2 t_2\) પરંતુ \(v_0 = 0\) છે.
\(\therefore \,{t_2}\, = \,\frac{\upsilon }{{g\,\sin \,{\theta _2}}}\,\,\, = \,\frac{{14.14}}{{10\,\sin \,{{60}^ \circ }}}\,\,\, = \,\frac{{2\sqrt 2 }}{3}\,\,\) સેકન્ડ
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$0.5 kg$ ના દડાને $14 m/s$ ના વેગથી ઉપર તરફ ફેંકતા $8 m$ ઊંચાઇ પર જાય છે.દડો ઉપર જાય તે દરમિયાન હવા દ્વારા કેટલા ........... $J$ ઊર્જાનો વ્યય થશે?View Solution
- 2બે $1 \;gm$ અને $4 \;gm$ ના દળ સમાન ગતિઊર્જાથી ગતિ કરે છે. તેમના રેખીય વેગમાનના મૂલ્યનો ગુણોત્તર કેટલો થાય?View Solution
- 3પદાર્થને ઉપર તરફ ફેંકતાં તેની મહત્તમ ઊંચાઇ $h$ છે.તો$\frac{{3h}}{4},$ઊંચાઇએ ગતિઊર્જા અને સ્થિતિઊર્જાનો ગુણોત્તરView Solution
- 4$m_1$ દળનો એક કણ $m_2$ દળના સ્થિર સ્થિતિએ રહેલા બીજાકણ સાથે સંપૂર્ણ અસ્થિતિ સ્થાપક હેડ ઓન સંઘાત અનુભવે છે. ($m_2$ > $m_1$). આ સંઘાતમાં ઘર્ષણની ગતિઊર્જા કેટલા મૂલ્યની ઉષ્માઊર્જામાં રૂપાંતરણ પામશે?View Solution
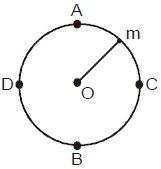
- 5View Solutionએક દળ શિરોલંબ વર્તુળમય ગતિ કરે છે (આકૃતિ જુઓ). જો કણનો સરેરાશ વેગ વધારવામાં આવે, તો દોરી કયા બિંદુ આગળ તૂટશે?
- 6$M$ દળનો એક કણ $R$ જેટલી નિશ્ચિત ત્રિજ્યા ના વર્તુળાકાર માર્ગ પર એવી રીતે ગતિ કરે છે કે $t$ સમયે કેન્દ્રગામી બળ $n^2Rt^2$ દ્વારા આપી શકાય જ્યાં $n$ એ અચળાંક છે.તો કણ પર લાગતાં બળ દ્વારા તેના પર અપાયેલ પાવર કેટલો હશે?View Solution
- 7જો પદાર્થની ગતિઊર્જામાં $300\%$ નો વધારો થાય, તો વેગમાનમાં થતો પ્રતિશત ફેરફાર કેટલો હશે?View Solution
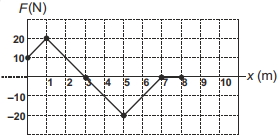
- 8આકૃતિ એ એક કાઝ પર $x$-અક્ષની સાપેક્ષે લાગતાં બળ $F$ માં થતો ફેરફાર દર્શાવે છે. જો કણએ $x=0$ પરથી સ્થિર સ્થિતિથી શરૂઆત કરે છે તો તે ફરીથી શુન્ય ઝડપ મેળવશે ત્યારે કણનાં યામાક્ષો શું હશે ?View Solution
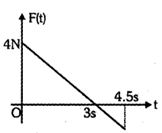
- 9$2 kg $ દળનો એક ટુકડો $x -$ અક્ષ સાથે મુક્ત રીતે ગતિ કરે છે. તે $t = 0$ સ્થાનેથી સ્થિર સ્થિતિએ છે. તે સમય બળ આધારિત આલેખની $x -$ દિશામાં ગોઠવાયેલો છે. બળ $F(t)$ સમય $t$ સાથે બદલાય છે જે આકૃતિમાં દર્શાવ્યું છે. $4.5$ સેકન્ડ પછી ટુકડાની ગતિ કેટલા ...$J$ હશે ?View Solution
- 10$F=\left(5+3 y^2\right)$ જેટલું બળ કણ ઉપર $y-$દિશામાં પ્રવર્તે છે, જ્યાં $F$ એ ન્યૂટનમાં અને $y$ એ મીટરમાં છે. $y=2\,m$ થી $y=5\,m$ સુધીના સ્થાનાંતર દરમિયાન બળ દ્વારા થતું કાર્ય $...........\,J$ થશે.View Solution
