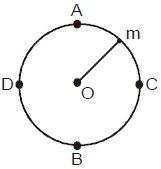
એક દળ શિરોલંબ વર્તુળમય ગતિ કરે છે (આકૃતિ જુઓ). જો કણનો સરેરાશ વેગ વધારવામાં આવે, તો દોરી કયા બિંદુ આગળ તૂટશે?

AIPMT 2000, Medium
b
Tension at any point in vertical motion is given by :
Tension at any point in vertical motion is given by :
\(T =\frac{ mv ^{2}}{ l }+ mg \cos \theta\)
\(\theta=\) angular displacement from lowest point,
\(l=\) length of string
\(m =\) mass of string
It is clear that tension at the lowest point \((B)\) is greatest than at other points (\(A, C , D\) ). If we increase average velocity, tension will increase at lowest point, therefore at point B, string has maximum possibility of break.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2\; m/s$ ના વેગથી ગતિ કરતા એક બોલ તેનાથી બમણા દળવાળા બીજા સ્થિર બોલ સાથે હેડ ઓન સંઘાત કરે છે. જો રેસ્ટિટયુશન ગુણાંકનુ મૂલ્ય $0.5$ હોય, તો અથડામણ બાદ બંને બોલના વેગ અનુક્રમે કેટલા થાય?View Solution
- 2$2\; kg$ દળનો $36 \;km/hr $ ના વેગથી ગતિ કરતો ધાતુનો ગોળો બીજા $3\; kg $ ના સ્થિર રહેલા ગોળા સાથે હેડ ઓન સંઘાત કરે છે. જો અથડામણ પછી બે બોલ સાથે ગતિ કરે તો અથડામણને કારણે ગતિઊર્જામાં થતો ધટાડો ($J$ માં) કેટલો હશે?View Solution
- 3$9.8\,kg$ દળ ધરાવતી રેતીની એક બેગને દોરડા વડે લટકાવેલ છે. $200\,g$ દળની અને $10\,ms ^{-1}$ ની ઝડપથી ગતિ કરતી બુલેટ (ગોળી) તેમાં ધૂસી જાય છે, તો ગતિઊર્જામાં થતો ધટાડો $.....\,J$ થશે.View Solution
- 4એક બાળક હીંચકા પર બેસીને હીંચકા ખાય છે. પૃથ્વીની સપાટીથી તેની ન્યુનતમ ઊંચાઇ અને મહત્તમ ઊંચાઇ અનુક્રમે $0.75\,m$ અને $2\,m$ છે. હીંચકાનો મહત્તમ વેગ ($m/s$ માં) કેટલો હશે?View Solution
- 5$1\, m$ લંબાઈ સાથે બાંધેલ એક નાનો ગોળો એક ઉર્ધ્વ વર્તુળ દર્શાવે છે કે જેથી દોરીઓમાં મહત્તમ અને ન્યૂનતમ તણાવનો ગુણોત્તર $5:1$ છે. ગોળાનો સૌથી ઉચ્ચતમ સ્થાન પાસે વેગ ............ $m /s$ છે. $(g =10\, m/s^2$ લો.)View Solution
- 6એક સાદા લોલકની લંબાઈ $75 cm$ છે. જે શિરોલંબ અર્ધ વર્તૂળ દર્શાવે છે. જ્યારે તે મધ્યવર્તૂળ સ્થાનેથી પસાર થાય ત્યારે દડાનો વેગ કેટલો હશે ?View Solution
- 7આ પ્રશ્ન વિધાન $1 $ અને વિધાન $2$ ધરાવે છે. વિધાનો બાદ આપેલા ચાર વિકલ્પોમાંથી બંને વિધાનોને સૌથી સારી રીતે સમજાવતો વિકલ્પ પસંદ કરો.જો અનુક્રમે બળ અચળાંકો $k_1$ અને $k_2$ ની બે સ્પ્રિંગ $S_1$ અને $S_2$ એક જ સમાન બળ વડે ખેંચવામાં આવી હોય, તો, માલુમ પડે છે કે, $S_2$ સ્પ્રિંગ પર થયેલા કાર્ય કરતાં $S_1$ સ્પ્રિંગ પર થયેલું કાર્ય વધારે છે.View Solution
વિધાન $- 1$: જો એક જ સમાન (બળના) જથ્થાથી ખેંચવામાં આવી હોય તો $S_1$ પર થયેલું કાર્ય, $S_2$ પર થયેલાં કાર્ય કરતાં વધારે છે.
વિધાન $- 2$:$ k_1 < k_2$
- 8View Solutionકોની હાજરીમાં કાર્ય-ઊર્જા પ્રમેય પ્રમાણભૂત (માન્ય) છે?
- 9લીફ્ટમાં $60\; HP$ ક્ષમતા ધરાવતી ઇલેક્ટ્રિક મોટર મહત્તમ $2000\; \mathrm{kg}$ ઉચકાવી શકે છે. જો લીફ્ટમાં ઘર્ષણબળ $4000 \;\mathrm{N}$ હોય તો મહત્તમ ક્ષમતાથી ભરેલ લિફ્ટ કેટલા ............. $\mathrm{m} / \mathrm{s}$ ના વેગથી ગતિ કરી શકે?View Solution
$\left(1 \;\mathrm{HP}=746 \;\mathrm{W}, \mathrm{g}=10\; \mathrm{ms}^{-2}\right)$
- 10$m$ દળનો એક ટુકડો $k$ સ્પ્રિંગ અચળાંકવાળી એક સ્પ્રિંગ કે જેનો એક છેડો દિવાલ સાથે જોડાયેલ છે તેની વિરૂદ્ધમાં ધકેલાય છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ટુકડો ઘર્ષણરહિત ટેબલ પર સરકે છે. સ્પ્રિંગની પ્રાકૃતિક લંબાઈ $l_0$ છે અને જ્યારે ટુકડો મુક્ત થાય છે ત્યારે તે તેની પ્રાકૃતિક લંબાઈની અડધી લંબાઈ જેટલી સંકોચાય છે તો ટુકડાનો અંતિમ વેગ કેટલો હશે ?View Solution