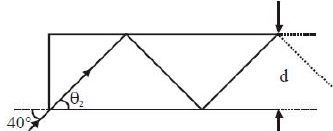
If we approximate the angle \(\theta_{2}\) as \(30^o\) initially then answer will be closer to \(57000\). but if we solve thoroughly, answer will be close to \(55000\) .
So both the answers must be awarded. Detailed solution as following.
Exact solution
By Snell's law \(1.\sin {40^o} = (1.31)\sin {\theta _2}\)
\(\sin \theta_{2}=\frac{64}{1.31}=\frac{64}{131} \approx .49\)
Now \(\tan {\theta _2} = \frac{{64}}{{\sqrt {{{(131)}^2} - {{(64)}^2}} }}\) \( = \frac{{64}}{{\sqrt {13065} }} \approx \frac{{64}}{{114.3}} = \frac{{\text{d}}}{x}\)
Now number of reflections
\(=\frac{2 \times 64}{114.3 \times 20 \times 10^{-6}}=\frac{64 \times 10^{5}}{114.3}\)
\(=55991 \approx 55000\)
Approximate solution
By Snell's law \(1 . \sin 40^{\circ}=(1.31) \sin \theta_{2}\)
\({\sin \theta_{2}=\frac{0.64}{1.31}=\frac{64}{131} \approx 0.49}\)
If assume \( \Rightarrow {\theta _2} \approx {30^o}\)
\(\tan {30^o} = \frac{{\text{d}}}{{\text{x}}} \Rightarrow {\text{x}} = \sqrt 3 {\text{d}}\)
Now number of reflections
\(=\frac{\ell}{\sqrt{3} \mathrm{d}}=\frac{2}{\sqrt{3} \times 20 \times 10^{-6}}=\frac{10^{5}}{\sqrt{3}}\)
\(\approx 57735 \approx 57000\)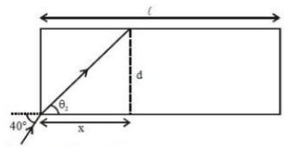
Download our appand get started for free
Similar Questions
- 1પ્રકાશનું કિરણ અરીસાના સમતલને લંબરૂપે આપાત થાય છે.તો પરાવર્તન કોણ ......$^o$ થશે.View Solution
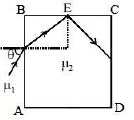
- 2$d$ બાજુ અને $\mu_2$ વક્રીભવનાંક ધરાવતા પારદર્શક ઘનને $\mu_1(\mu_1 < \mu_2)$ વક્રીભવનાંક ધરાવતા પ્રવાહીમાં મુકેલ છે આકૃતિમાં દર્શાવ્યા પ્રમાણે $AB$ બાજુ પરથી એક પ્રકાશનું કિરણ $\theta $ ખૂણે આપત કરવામાં આવે છે જે $BC$ બાજુ પર $E$ બિંદુ આગળ પૂર્ણ આંતરિક પરાવર્તન પામે છે. આ માટે $\theta $ નું મૂલ્ય કેટલું હોવું જોઈએ?View Solution
- 3$30 \,cm$ કેન્દ્રલંબાઈ ધરાવતા એક બહિર્ગોળ લેન્સથી $60\, cm$ અંતરે એક બિંદુવત વસ્તુ રાખવામાં આવેલ છે. જે એક સમતલ અરીસાને લેન્સની મુખ્ય અક્ષને લંબરૂપે અને તેનાથી $40\, cm$ અંતરે મૂકવામાં આવતા, અંતિમ પ્રતિબિંબ $....$ અંતરે રચાશે.View Solution

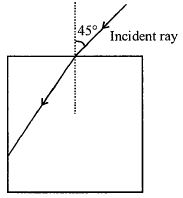
- 4View Solutionઆકૃતિમાં દર્શાવ્યા પ્રમાણે એક પ્રકાશનું કિરણ એક કાચના સ્લેબ પર પડે છે. જો શિરોલંબ સપાટી પર પૂર્ણ આંતરિક પરાવર્તન કરવું હોય તો કાચનો વક્રીભવનાંક કેટલો હશે?
- 5કાટખૂણો ધરાવતા પ્રિઝમની એક બાજુને લંબ રૂપે પ્રકાશ આપાત કરતાં તે પ્રિઝમમાં પાયાને સમાંતર ગતિ કરે છે. જો પ્રિઝમનો વક્રીભવનાંક $\mu$ હોય,તો કર્ણએ પાયા સાથે બનાવેલ ખૂણો કેટલો રાખવાથી કિરણ કર્ણ દ્વારા સંપૂર્ણ પરાવર્તન પામે?View Solution
- 6$30^o $ પ્રિઝમકોણ માટે $45^o $ આપાતકોણ છે.કિરણ $AC$ દ્વારા પરાવર્તન થઇને મૂળ માર્ગે પાછો ફરે છે. તો પ્રિઝમનો વક્રીભવનાંક કેટલો હશે?View Solution
- 7$60^°$ ના ખૂણે રહેલા બે સમતલ અરીસા પર એક કિરણ $50^°$ ના ખૂણે આપાત કરવામાં આવે છે.તે પરાવર્તન પામીને બીજા અરીસા પર આપાત થાય છે.ત્યાંથી પરાવર્તન પામીને પ્રથમ અરીસા પર ......$^o$ ના ખૂણે આપાત થશે?View Solution
- 8સંયુકત માઇક્રોસ્કોપમાં ઓબ્જિેકિટવપીસ અને આઇપીસની મોટવણી $m_1$ અને $m_2$ છે.તો સંયુકત માઇક્રોસ્કોપની મોટવણી કેટલી થાય?View Solution
- 9$40cm$ વક્રતાત્રિજયા ધરાવતા અંર્તગોળ અરીસા દ્વારા પ્રતિબિંબની ઊંચાઇ વસ્તુ કરતાં બમણી મેળવવા માટે,વસ્તુ અંતર કેટલા ......$cm$ હોવું જોઈએ?View Solution
- 10ટેલિસ્કોપના વસ્તુકાંચની કેન્દ્રલંબાઈ $150\,\,cm$ અને નેત્રકાંચની કેન્દ્રલંબાઈ $5 \,\,cm$ છે. જો $1\,\,km$ અંતરે રહેલ $50\,\,m$ ઊંચી વસ્તુને આ ટેલિસ્કોપ વડે જોવામાં આવે ત્યારે ટાવરના પ્રતિબિંબ વડે બનતો ખૂણો $\theta $, હોય તો $\theta $ નું મૂલ્ય $^o$ માં લગભગ કેટલું હશે?View Solution
