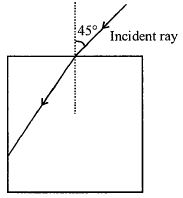
At point A by Snell's law
\(\mu=\frac{\sin 45^o}{\sin r} \Rightarrow \sin r=\frac{1}{\mu \sqrt{2}}\) ..... \((i)\)
At point \(B\), for total internal reflection,
\(\sin {i_1} = \frac{1}{\mu }\)
From figure, \(\mathrm{i}_{1}=90^{\circ}-\mathrm{r}\)
\(\therefore \) \(\left(\sin 90^o-r\right)=\frac{1}{\mu}\)
\(\Rightarrow \cos r=\frac{1}{\mu}\) ...... \((ii)\)
Now \(cos\,r\,=\,\sqrt{1-\sin ^{2} r}=\sqrt{1-\frac{1}{2 \mu^{2}}}\)
\(=\sqrt{\frac{2 \mu^{2}-1}{2 \mu^{2}}}\) ...... \((iii)\)
From eqs \((ii)\) and \((iii)\)
\(\frac{1}{\mu}=\sqrt{\frac{2 \mu^{2}-1}{2 \mu^{2}}}\)
Squaring both sides and then solving, we get
\(\mu=\sqrt{\frac{3}{2}}\)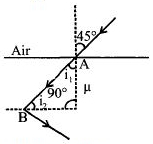
Download our appand get started for free
Similar Questions
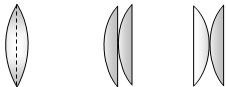
- 1View Solutionબે સમાન સમતલ બર્હિગોળ લેન્સને આકૃતિ મુજબ મૂકતાં તેમની કેન્દ્રલંબાઇનો ગુણોત્તર કેટલો થાય?
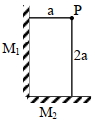
- 2બે સમતલ અરીસા ${M}_{1}$ અને ${M}_{2}$ આકૃતિમાં દર્શાવ્યા પ્રમાણે એકબીજાને લંબ મૂકેલા છે. બિંદુવત ઉદગમ $P$ ને ${M}_{1}$ અને ${M}_{2}$ અરિસાથી અનુક્રમે $a$ અને $2a$ મીટર અંતરે મૂકેલા છે. બનતા પ્રતિબિંબો વચ્ચેનું મહત્તમ અંતર કેટલું હશે? ($\sqrt{5}=2.3$ )View Solution
- 3$8\,ms ^{-1}$ ના નિયમિત વેગથી ઉર્ધ્વદિશા ઉપર તરફ તરતી એક માછલી એવું જુએ છે કે એક પક્ષી માછલી તરફ $12\,ms ^{-1}$ ના વેગથી અધોદિશામાં ડુબકી મારી રહયું છે. જો પાણીની વક્રીભવનાંક $\frac{4}{3}$ હોય, તો પક્ષીની માછલીને પકડવા માટેની ડ્રાઈવનો સાચો વેગ ......... $ms ^{-1}$ હશે.View Solution
- 4નીચે બે વિધાનો આપેલા છે -View Solution
વિધાન $I$: જ્યારે સફેદ પ્રકાશ પ્રિઝમમાંથી પસાર થાય છે ત્યારે રાતો પ્રકાશ પીળા અને જાંબલી પ્રકાશ કરતાં વધારે વાંકો વળે છે.
વિધાન $II$ : વિભાન કરી શકતાં માધ્યમાં જુદી-જુદી તરંગલંબાઈ માટે જુદા-જુદા વક્રીભવનાંક હોય છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીયે આાપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો -
- 5View Solutionપ્રકાશનાં કોર્પ્યુસ્કુલર સિદ્ધાંત મુજબ પ્રકાશની ઝડપ
- 6$\frac{5}{3}$ વક્રીભવનાંક ધરાવતા પાણીની સપાટીથી $4 \,m$ ઊંડાઈએ એક બિંદુવત પ્રકાશ ઉદ્ગમ છે. પાણીની મુકત સપાટી પરથી બહાર આવતો પ્રકાશ અટકાવવા માટે ઉદ્ગમસ્થાનની બરાબર ઉપર, પાણીની સપાટી પર કેટલા વ્યાસવાળી ($m$ માં) અપારદર્શક તકતી મૂકવી જોઇએ?View Solution
- 7માછલી $\sqrt 7 \,cm$ ઊંડાઇ પર છે.તો તે બહાર જોઇ શકતા ક્ષેત્રફળની ત્રિજયા કેટલા ......$cm$ હશે?View Solution
- 8View Solutionજ્યારે પાતળા બહિર્ગોળ લેન્સ ને તેટલી જ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાના સંપર્કમાં મૂકવામાં આવે છે. તંત્રની પરિણામી કેન્દ્રલંબાઈ ......છે.
- 9સ્થાનાંતર રીતમાં $f$ કેન્દ્રલંબાઈના લેન્સનો ઉપયોગ કરવામાં આવે છે અને વસ્તુ અને પડદા વચ્ચેનું અંતર $60\, cm$ છે. કેન્દ્રલંબાઈનું શક્ય મૂલ્ય ........ $cm$ છે ?View Solution
- 10$8m$ ઊંડાઇ ધરાવતી ટાંકીમાં પાણી ($\mu = 4/3$) ભરેલ છે.તો તળિયું કેટલી ઊંડાઇ પર દેખાય?View Solution
