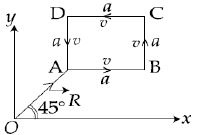
આકૃતિમાં દર્શાવ્યા પ્રમાણે $m$ દ્રવ્યમાનનો એક કણ સમાન ઝડપ $v$ થી $a$ બાજુ ધરાવતા ચોરસની બાજુ પર $x-y$ સમતલમાં ફરે છે. તો નીચે આપેલ વિધાનોમાંથી કયું વિધાન મૂળબિંદુની ફરતે કોણીય વેગમાન $\vec L$ માટે ખોટું છે?

JEE MAIN 2016, Diffcult
d
\(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{P}}\) or \(\overrightarrow{\mathrm{L}}=\mathrm{rpsin} \theta \hat{\mathrm{n}}\)
\(\overrightarrow{\mathrm{L}}=\overrightarrow{\mathrm{r}} \times \overrightarrow{\mathrm{P}}\) or \(\overrightarrow{\mathrm{L}}=\mathrm{rpsin} \theta \hat{\mathrm{n}}\)
\(\overrightarrow{\mathrm{L}}=\mathrm{r}_{\perp}(\mathrm{P}) \hat{\mathrm{n}}\)
For \(D\) to \(A\)
\(\overrightarrow{\mathrm{L}}=\frac{\mathrm{R}}{\sqrt{2}} \mathrm{mV}(-\hat{\mathrm{k}})\)
For \(A\) to \(B\)
\(\overrightarrow{\mathrm{L}}=\frac{\mathrm{R}}{\sqrt{2}} \mathrm{mV}(-\hat{\mathrm{k}})\)
For \(\mathrm{C}\) to \(\mathrm{D}\)
\(\overrightarrow{\mathrm{L}}=\left(\frac{\mathrm{R}}{\sqrt{2}}+\mathrm{a}\right) \mathrm{mV}(\hat{\mathrm{k}})\)
For \(B\) to \(C\)
\(\overrightarrow{\mathrm{L}}=\left(\frac{\mathrm{R}}{\sqrt{2}}+\mathrm{a}\right) \mathrm{mV}(\hat{\mathrm{k}})\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$HCL $ અણુમાં બે પરમાણુ વચ્ચેનું અંતર $1.27\ Å$ છે. $Cl$ પરમાણુનું દળ $H $ પરમાણુ કરતા $35.5$ ગણું છે.તો $H$ પરમાણુથી દ્રવ્યમાન કેન્દ્રનું અંતર ...... $\mathop A\limits^o $ થાય.View Solution
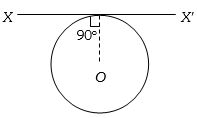
- 2$L$ લંબાઇ અને $\rho $ રેખીય ઘનતા ધરાવતા તારને વર્તુળમાં વાળતાં $XX'$ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
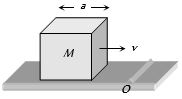
- 3$a$ બાજુવાળો એક સમઘન નીચેની આકૃતિમાં દર્શાવ્યા પ્રમાણે એક સમક્ષિતિજ સમતલ પર $v$ વેગથી ગતિ કરે છે તે $O$ બિંદુ આગળ આકૃતિમાં દર્શાવ્યા પ્રમાણે એક ઊપસેલી સપાટી પાસેથી પસાર થાય તો $O$ બિંદુ પછી તેનો કોણીય વેગ કેટલો થાય ?View Solution
- 4View Solutionએક કણ નિયમિત વર્તુળાકાર ગતિ માંથી પસાર થાય છે. વર્તુળના સમતલ માં ક્યા બિંદુ એ કણનો કોણીય વેગમાન સંરક્ષિત (અચળ) હશે ?
- 5$1\,kg$ દળ અને $R$ ત્રિજ્યયા ઘરાવતી તક્તિ તેના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ તેવી સમક્ષિતિજ અક્ષને અનુલક્ષીને પરિભ્રમણ કરવા મુક્ત છે. તક્તિ જેટલું દળ ધરાવતી વસ્તુને તક્તિનાં સૌથી ઉપરના છેડા આગળ જોડવામાં આવે છે. હવે આ તંત્રને છોડવામાં આવે છે, જયારે વસ્તુ સૌથી નીચેના છેડે આવે છે ત્યારે કોણીય ઝડપ $4 \sqrt{\frac{x}{3 R}} rad s ^{-1}$ થાય છે.$x$નું મૂલ્ય $.......$ થશે.View Solution
$[\left.g =10\,m / s ^{2}\right]$
- 6એક પદાર્થ માત્ર કોણીય ગતિ કરે છે જો કણ નો રેખીય વેગ $v$ અને તે $x$-અક્ષ થી $r$ અંતરે $\omega $ કોણીય વેગ થી ફરતો હોય $\omega = \frac{v}{r}$ હોય તો પદાર્થ માટે શું સાચું છે ?View Solution
- 7$2.4\ kg-m^2$ જડત્વની ચાકમાત્રા ધરાવતા સ્થિર પદાર્થમાં $750\ J$ ચાકગતિ ઊર્જા ઉત્પન્ન કરવા માટે $5\ rad/s^2$ નો કોણીય પ્રવેગ ........ $(\sec)$ સમય સુધી આપવો પડે.View Solution
- 8ઘન નળાકારની તેની અક્ષ પર જડત્વની ચાકમાત્રાએ તેના ગુરૂત્વકેન્દ્રમાંથી પસાર થતી અને તેની લંબાઈને લંબ અક્ષ પરની જડત્વની ચાકમાત્રા જેટલી છે. લંબાઈ $ L$ અને ત્રિજ્યા $ R $ વચ્ચેનો સંબંધ શું થશે ?View Solution
- 9કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ તેવી અક્ષને અનુલક્ષીને એક પાતળી નિયમિત તકતીની ચક્રાવર્તન ત્રિજ્યા અને તકતીના વ્યાસને ફરતે ચક્રાવર્તન ત્રિજ્યાનો ગુણોતર $......$ હશે.View Solution
- 10$5 \mathrm{~kg}$ દળ ધરાવતો પદાર્થ $3 \sqrt{2} \mathrm{~ms}^{-1}$ ની સમાન ઝડપ સાથે $X-Y$ સમતલમાં $y=x+4$ રેખાની દિશામાં ગતિ કરે છે. ઉગમબિંદુને અનુલક્ષીને કણનું કોણીય વેગમાન__________$\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-1}$ થશે.View Solution
