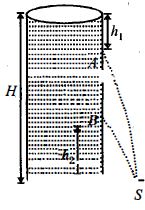
આકૃતિમાં દર્શાવ્યા પ્રમાણે નળાકાર ટાંકીની દીવાલમાં $A$ અને $B$ સપાટીથી $h_1$ ઊંડાઈ અને તળિયેથી $h_2$ ઊંચાઈ પર બે હૉલ છે.પાણીની સપાટી ટાંકીના તળિયેથી $H$ ઊંચાઈ પર છે.બંને હૉલમાંથી આવતું પાણી જમીન પર સમાન સ્થાન $S$ પર પડે છે તો $h_1$ અને $h_2$ નો ગુણોત્તર કેટલો થાય?
AIEEE 2012, Diffcult
Download our app for free and get started
a
Range is same for both holes
Range is same for both holes
\(\therefore \,2\sqrt {(H - {h_1}){h_1}} = 2\sqrt {\left( {H - {h_2}} \right){h_2}} \)
Squaring both sides,
\(4\left( {H - {h_1}} \right){h_1} = 4\left( {H - {h_2}} \right){h_2}\)
\(H{h_1} - h_1^2 = H{h_2} - h_2^2\)
On solving we get,
\(H = {h_1} + {h_2}\)
Hence, the ratio of \(\frac{{{h_1}}}{{{h_2}}}\) depends on \(H\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાણી સપાટ તળીયું ધરાવતી એક મોટી ટાંકીમાં $10^{-4}\,m/s$ ના દરથી વહે છે. ઉપરાંત, તળીયામાં $1\, cm^2$ ક્ષેત્રફળ ધરાવતા છિદ્રમાંથી વહી (લિક) જાય છે. જો ટાંકીમાં પાણીની ઊંચાઈ અચળ જળવાતી હોય તો આ ઊંચાઈ ........ $cm$ હશે.View Solution
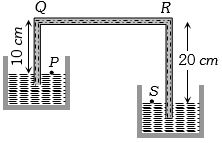
- 2પ્રવાહીની ઘનતા $ 1.5 gm/cc$ છે,તો $P$ અને $S$ બિંદુ વચ્ચે દબાણનો તફાવત કેટલો થાય?View Solution
- 3ગોળાકાર વરસાદના ટીપાંનો અંતિમ (ટર્મીનલ) વેગ ($v_t$) ધણાં બધા પ્રાચલો ઉપર આધાર રાખે છે. પરંતુ $\left(v_{t}\right)$ નો ગોળાકાર વરસાદના ટીપાંની ત્રિજ્યા $(r)$ સાથેનો ફેરફાર......... પર આધાર રાખે છે.View Solution
- 4$60\, kg$ દળ ધરાવતો છોકરો નદીમાં લાકડાના સહારે તરવા માંગે છે.જો લાકડાની સાપેક્ષ ઘનતા $0.6$ હોય તો લાકડાનું ઓછામાં ઓછું કદ કેટલું હોવું જોઈએ? (નદીના પાણીની ઘનતા $1000\, kg/m^3$)View Solution
- 5નળાકાર ટયુબ $AB$ માં $ A$ છેડે પાણી ${v_1}$ વેગથી દાખલ થાય છે, અને $ B$ છેડે પાણી ${v_2}$ વેગથી બહાર આવે છે,પ્રથમ કિસ્સા $I$ માં નળી સમક્ષિતિજ રાખેલ છે,બીજા કિસ્સા $ II $ માં નળીનો $ A $ છેડો ઉપર રહે,તેમ શિરોલંબ રાખેલ છે,ત્રીજા કિસ્સા $ III $ માં નળીનો $B $ છેડો ઉપર રહે,તેમ શિરોલંબ રાખેલ છે.તો કયા કિસ્સા માટે ${v_1} = {v_2}$ થાય?View Solution
- 6એક હાઈડ્રોલીક પ્રેસ $100\, kg$ ને ઊંચકી શકે છે જ્યારે $‘m'$ જેટલું દળ નાના પિસ્ટન પર મૂકવામાં આવે છે. દળ ને $‘m’$ જેટલું સમાન રાખીને જો મોટા પીસ્ટનનો વ્યાસ $4$ ગણો વધારવામાં આવે અને નાના પીસ્ટનનો વ્યાસ $4$ ગણો ઘટાડવામાં આવે તો તે ............... $kg$ દળ ઊંચકી શકશે.View Solution
- 7અનુક્રમે $2 \times 10^{-2}\,m$ અને $4 \times 10^{-2} \,m$ વ્યાસ ધરાવતીને પાણીની પાઈપો $P$ અને $Q$ ને પાણીની મુખ્ય પ્રવાહ રેખા સાથે શ્રેણીમાં જોડવામાં આવે છે. $P$ પાઈપમાંથી વહન થઈ રહેલા પાણીનો વેગ એ .............View Solution
- 8તળાવની અડધી ઊંડાઇએ દબાણ તળિયા કરતાં $2/3$ ગણું છે,તો તળાવની ઊંડાઇ ....... $m$ હશે .View Solution
- 9View Solutionતળાવમાં તરતી બોટમાં એક લોખંડનો ટુકડો રાખેલ છે. જો આ ટુકડાને તળાવમાં નાખવામાં આવે તો પાણીનું લેવલ
- 10પાણીની ટાંકીના તળિયે છિદ્ર છે.તળિયે કુલ દબાણ $3\, atm (1\, atm = 10^{5}N/m^{2})$ છેે.તો છિદ્રમાંથી બહાર આવતા પાણીનો વેગ કેટલો થાય?View Solution