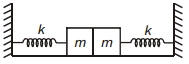
આકૃતિનાં દર્શાવ્યા મુજબની જ પૃથ્વીની સપાટીને સમક્ષિતિજ રહે તેમ ગોઠવવામાં આવેલ છે. આ સ્થિતિમાં સ્પ્રિંગો પર કોઈ તણાવ નથી સામાન્ય સ્થિતિમાં છે. જો ડાબી તરફનું દળ ડાબી તરફ અને જમણી તરફનું દળ જમણી તરફ સરખા અંતેર ખેંચીને છોડવામાં આવે છે. જો પરિણામી અથડામણ સ્થિતિ સ્થાપક હોય તો આ પ્રણાલીના દોલનોનો આવર્તકાળ કેટલો હશે ?
Medium
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સાદા આવર્ત દોલક માટે વ્યાપક સ્થાનાંતર $x= A \sin \omega t$ છે. ધારો કે $T$ તેનો આવર્તક છે. તેની સ્થિતિઊર્જા $(U)$ - સમય $(t)$ ના વક્રનો ઢાળ, જ્યારે $t=\frac{T}{\beta}$ થાય ત્યારે, મહતમ થાય છે. $\beta$નું મૂલ્ય $..............$ છે.View Solution
- 2${\sin ^2}(\omega t)$ વિધેય દર્શાવે છે.કે...View Solution
- 3View Solutionઅવમંદિત દોલનના કિસ્સામાં દોલકની આવૃત્તિ
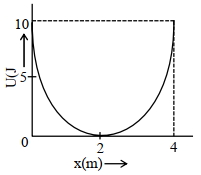
- 4$5\, {kg}$ દળને સ્પ્રિંગ સાથે જોડેલ છે. આ તંત્ર દ્વારા થતી સરળ આવર્તગતિની સ્થિતિઊર્જાનો ગ્રાફ આકૃતિમાં દર્શાવેલ છે. $4\, {m}$ લંબાઈના સાદા લોલકનો આવર્તકાળ સ્પ્રિંગતંત્રના આવર્તકાળ જેટલો જ છે. જ્યાં આ પ્રયોગ કરવામાં આવેલ છે તે ગ્રહ પર ગુરુત્વપ્રવેગનું મૂલ્ય (${m} / {s}^{2}$ માં) કેટલું હશે?View Solution
- 5$200\; gm$ ના દળને $80 \;N/m$. બળઅચળાંક ઘરાવતી સ્પ્રિંગ પર લટકાવેલ છે તેનો આવર્તકાળ કેટલો ..... $\sec$ થાય?View Solution
- 6View Solutionનીચે પૈકી કયું સરળ આવર્તગતિનું ઉદાહરણ છે?
- 7View Solutionપ્રણોદિત દોલનોના કિસ્સામાં અનુનાદ તરંગ તીક્ષ્ણ બને જ્યારે .....
- 8સરળ આવર્ત ગતિનું સમીકરણ $ x = 0.01\cos \left( {\pi \,t + \frac{\pi }{4}} \right) $ હોય,તો આવૃત્તિ કેટલી થાય?View Solution
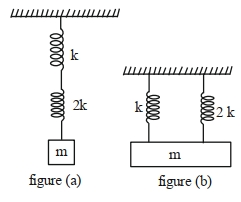
- 9આપેલ પરિપથ મુજબ, $k$ અને $2 k$ જેટલો સ્પ્રિંગ અચળાંક ધરાવતી બે સ્પ્રિંગોને દળ $m$ સાથે જોડવામાં આવેલ છે. જો આકૃતિ $(a)$ માં દોલનોનો આવર્તકાળ $3s$ હોય તો આકૃતિ $(b)$ માં દોલનોનો આવર્તકાળ $\sqrt{x} s$ છે. $x$ નું મૂલ્ય થશે.View Solution
- 10$A$ જેટલો આડછેદ ધરાવતા એક સમાંગ તારમાંથી બનાવેલા સાદા લોલકનો આવર્તકાળ $T$ છે.જયારે વધારાનું દળ $M$ દોલકમાં ઉમેરવામાં આવે છે,ત્યારે તેનો આવર્તકાળ બદલાઇ $TM$ થાય છે.જો તારના દ્વવ્ય માટે યંગનો સ્થિતિસ્થાપકતા અંક થ હોય,તો $\frac{1}{Y}$ _______ જેટલો થશે. ( $g$ ગુરુત્વીય પ્રવેગ છે.)View Solution