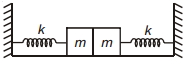
આકૃતિનાં દર્શાવ્યા મુજબની જ પૃથ્વીની સપાટીને સમક્ષિતિજ રહે તેમ ગોઠવવામાં આવેલ છે. આ સ્થિતિમાં સ્પ્રિંગો પર કોઈ તણાવ નથી સામાન્ય સ્થિતિમાં છે. જો ડાબી તરફનું દળ ડાબી તરફ અને જમણી તરફનું દળ જમણી તરફ સરખા અંતેર ખેંચીને છોડવામાં આવે છે. જો પરિણામી અથડામણ સ્થિતિ સ્થાપક હોય તો આ પ્રણાલીના દોલનોનો આવર્તકાળ કેટલો હશે ?

Medium
c
(c)
(c)
If there was no collision each spring will oscillate with period
\(T=2 \pi \sqrt{\frac{m}{k}}\)
Because of collisions the springs are only compressed but cannot extend beyond their natural length. Hence the perform only half oscillation.
Hence \(\quad T=2 \pi \sqrt{\frac{m}{k}} \div 2\)
or \(T=\pi \sqrt{\frac{m}{k}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે લંબ રીતે સરળ આવર્ત ગતિ કરતાં પદાર્થ માટે સમીકરણ નીચે આપેલા છે.તેમને જોડીને Lissajous ગ્રાફ બનાવવામાં આવે છે.View Solution
$x\left( t \right) = A\,\sin \,\left( {at + \delta } \right)$
$y\left( t \right) = B\,\sin \,\left( {bt} \right)$
તો નીચેનામાંથી શું સાચું પડશે?
- 2એક કણ $4 \mathrm{~cm}$ ના કંપવિસ્તારથી સરળ આવર્ત ગતિ કરે છે. મધ્યમાન સ્થાને કણનો વેગ $10 \mathrm{~cm} / \mathrm{s}$ છે. જ્યારે કણની ઝડ૫ $5\ \mathrm{cm} / \mathrm{s}$ થાય ત્યારે મધ્યમાન સ્થાન થી તેનું અંતર $\sqrt{\alpha}\ \mathrm{cm}$ છે,જ્યા $\alpha=$_______.View Solution
- 3એક કણ સુરેખ પથ પર સરળ આવર્તગતિ કરે છે. તેનો કંપવિસ્તાર $2 \,cm$ છે. જ્યારે મધ્યબિંદુ તેનું અંતર $1 \,cm$ અને વેગ અને પ્રવેગનાં મુલ્યો સરખા હોય તો તેનો આવર્તકાળ શોધો.View Solution
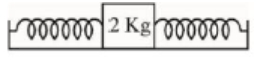
- 4$2\,kg$ દળ ધરાવતા બ્લોકને $20\,N / m$ સ્પ્રિંગ અચળાંક ધરાવતી બે સમાન સ્પ્રિંગ સાથે જોડવામાં આવે છે. બ્લોકને ધર્ષણ રહિત સપાટી પર મૂકવામાં આવે છે અને સ્પ્રિંગના છેડાને જડ આધાર સાથે લગાડવામાં આવે છે. (આકૃતિમાં જુઓ).જ્યારે દળને સંતુલન સ્થિતિમાંથી સ્થાનાંતરિત કરવામાં આવે ત્યારે તે સરળ આવર્ત ગતિ કરે છે. દોલનોનો આવર્ત કાળ $\frac{\pi}{\sqrt{x}}$ છે. તો $x$ નું મૂલ્ય $...........$ છે.View Solution
- 5જો કોઈ સમયે સરળ આવર્તગતિ કરતાં દોલકનું સ્થાનાંતર $0.02\;m$ અને પ્રવેગ $2\; m/s^2$ ને બરાબર થાય, તો દોલકની કોણીય આવૃત્તિ ($rad\,{s^{ - 1}}$ માં) કોને બરાબર થાય?View Solution
- 6સરળ આવર્ત ગતિ કરતાં પદાર્થની સ્થિતિઊર્જા સમતોલન સ્થાનથી કંપવિસ્તારના અડધા અંતરે $2.5\, J$ છે,તો કુલઊર્જા કેટલી .... $J$ થાય?View Solution
- 7સમતોલન સ્થાન પાસેથી સરળ આવર્ત ગતિ શરૂ કરતાં પદાર્થનો કંપવિસ્તાર $a$ અને આવર્તકાળ $T$ છે.સમતોલન બિંદુથી અડધા કંપવિસ્તાર સુધી પહોંચવા માટે કેટલો સમય લાગે?View Solution
- 8સ્પ્રિંગ સાથે લટકાવેલ દળનો આવર્તકાળ $T$ છે. જો સ્પ્રિંગને ચાર સમાન ભાગોમાં કાપવામાં આવે અને તે સમાન દળને એક ભાગ સાથે લટકાવવામાં આવે, તો નવો આવર્તકાળ કેટલો થાય?View Solution
- 9$\mathrm{m}$ દળને અવગણ્ય દળ ધરાવતી સ્પ્રિંગ સાથે લટકાવવામાં આવે છે અને આ તંત્ર $f_1$ આવૃત્તિ થી દોલનો કરે છે. જો $9 \mathrm{~m}$ ના દળને આ જ સ્પ્રિંગ પર લટકાવતા દોલનોની આવૃત્તિ $f_2$ થાય છે.______$\frac{f_1}{f_2}$ નું મૂલ્ય હશે.View Solution
- 10પુન: સ્થાપક બળ સ્થાનાંતરના સપ્રમાણમાં અને અવરોધક બળ વેગના સપ્રમાણમાં હોય તેવા કણ પર $Fsin\omega t$ બળ લાગે છે. જો કણનો કંપવિસ્તાર $\omega = {\omega _1}$ માટે મહત્તમ અને કણની ઊર્જા $\omega = {\omega _2}$ માટે મહત્તમ હોય, તો ........ (જ્યાં $\omega_0$ દોલન કરતાં કણની પ્રાકૃતિક આવૃતિ છે)View Solution
