આલેખ વડે દર્શાવેલ વિદ્યુતપ્રવાહ ફેરફાર માટે અર્ધચક્ર માટે વિદ્યુતપ્રવાહના મૂલ્યનો સરેરાશ કેટલો છે ?
Medium
Download our app for free and get started
a
(a)
(a)
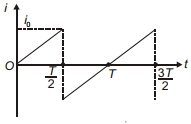
\(l_{\max }=\frac{\int \limits_0^{T / 2} / d t}{T / 2}\)
From 0 to \(\frac{T}{2}\) graph is straight line so the function \((l)\) will be \(=\frac{i_0}{(T / 2)} t=\frac{2 i_0}{T} t\)
\(\text { So }\)
\(l_{\text {mean }}=\frac{2}{T} \int \limits_0^{T / 2} \frac{2 i_0}{T} t d t=\frac{2}{T}\left(\frac{2}{T}\right) i_0\left(\frac{t^2}{2}\right)_0^{T / 2}\)
\(=\frac{4}{T^2} i_0\left(\frac{1}{2}\right)\left(\frac{T^2}{4}-0\right)=\frac{i_0}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$LC$ પરિપથમાં ઇન્ડક્ટર $L=40\;mH$ અને કેપેસીટર $C=100\;\mu F$ છે.જો પરિપથમાં $V(t)=10sin(314t)$ વૉલ્ટેજ આપવામાં આવે તો પરિપથમાંથી કેટલો પ્રવાહ પસાર થશે?View Solution
- 2$t =0$ સમયે કેપેસિટરમાં મહતમ ઊર્જા છે,તો કેટલા સમય પછી પરિપથમાં મહતમ પ્રવાહ થાય.View Solution
- 3નીચે બે વિધાનો આપેલા છે:View Solution
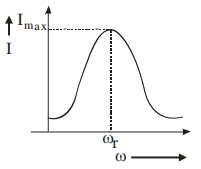
વિધાન $I$ : $LCR$ શ્રેણી પરિપથમાં, અનુનાદ વખતે મહત્તમ પ્રવાહ મળે છે.
વિધાન $II$ : જ્યારે બંનેને સમાન વોલ્ટેજ ઉદ્રગમ સાથે જોડેલા હોય ત્યારે ફક્ત અવરોધ ધરાવતા પરિપથ માં $LCR$ પરિપથ કરતાં કદાપી ઓછl પ્રવાહ મળશે નહી.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીયે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરોઃ
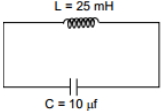
- 4$LCR$ પરિપથ માટે, $I$ વિરૂધ્ધ $\omega$ નો આલેખ દર્શાવેલ છે.View Solution
$(a)$ $\omega_{r}$ થી ડા.બા. પરિપથ મુખ્યત્વે સંધારક્ત (capacitive) ધરાવતો હશે.
$(b)$ $\omega_{r}$ થી ડા.બા. પરિપથ મુખ્યત્વે ઇન્ડક્ટીવ હશે.
$(c)$ $\omega_{ r }$ આગળ, પરિપથનો અવબાધ તેના અવરોધ જેટલો હશે.
$(d)$ $\omega_{ r }$ આગળ, પરિપથનો અવબાધ શૂન્ય હશે.
આપેલા વિકલ્પોમાંથી યોગ્ય ઉત્તર પસંદ કરો
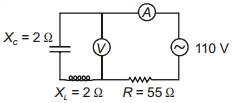
- 5પરિપથમાં એેમીટરનું વાંચન $...........A$ છે.View Solution
- 6$L-C-R$ પરિપથમાં $C = 10^{-11}\,Farad.$ $L = 10^{-5}\,Henry$ અને $R =100\,Ohm$ છે જ્યારે આ પરિપથને અચળ $E$ વૉલ્ટેજ ધરાવતા $D.C.$ સ્ત્રોત સાથે જોડવામાં આવે તો કેપેસીટર $10^{-9}\,C$ જેટલો વિજભાર પ્રાપ્ત કરે છે. આ $D.C.$ સ્ત્રોતને $sin$ વિધેય પર આધારિત વૉલ્ટેજ સ્ત્રોત સાથે જોડવામાં આવે છે જેનો મહત્તમ વૉલ્ટેજ $E_0$ એ $D.C.$ સ્ત્રોતના અચળ વૉલ્ટેજ $E$ જેટલો છે. અનુનાદ સમયે કેપેસીટર દ્વારા પ્રાપ્ત થતાં મહત્તમ વિજભારનું મૂલ્ય કેટલું હશે?View Solution
- 7$LCR$ શ્રેણી પરિપથ $(R=100Ω)$ ને $200\,v,\,300\,Hz$ આવૃતિવાળા $A.C$ ઉદ્ગમ સાથે જોડવામાં આવે છે.જયાર કેપેસિટરને દૂર કરવામાં આવે છે,ત્યારે વોલ્ટેજ કળામાં પ્રવાહ કરતાં $60^°$ આગળ છે. જયારે ઇન્ડકટરને દૂર કરવામાં આવે છે,ત્યારે પ્રવાહ કળામાં વોલ્ટેજ કરતાં $60^°$ આગળ છે.તો $LCR$ શ્રેણી પરિપથમાં પાવર કેટલા .....$W$ થાય?View Solution
- 8એક $LC$ દોલકમાં, જો ઈન્ડકટર અને સંધારકનું મૂલ્ય અનુક્રમે બમણું અને આઠગણું કરવામાં આવે તો દોલકની આવૃત્તિ તેની મૂળ પ્રાકૃતિક આવૃત્તિ $\omega_0$ કરતા $x$ નું મુલ્ય $.........$ થશે.View Solution
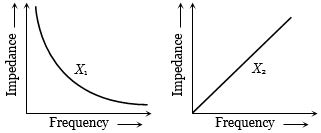
- 9View Solutionબે પરિપથના ઇમ્પિડન્સ વિરુધ્ધ આવૃત્તિનો આલેખ આપેલા છે,તો...
- 10એક $LCR$ પરિપથને $200 \mathrm{~V}, 50 \mathrm{~Hz}$ ના $ac$ ઉદગમ સાથે જોડવામાં આવેલ છે. જો પ્રેરક (ઈન્ડકટર) ($L=10mH$) ને સમાંતર વોલ્ટેજ $31.4 \mathrm{~V}$ હોય તો પરિપથમાં. . . . . પ્રવાહ વહેતો હશે.View Solution