આપેલ આકૃતિમાં, એક ઈન્ડકટર અને અવરોધને, $E$ વોલ્ટ $emf$ ધરાવતી બેટરી સાથે શ્રેણીમાં જોડવામાં આવે છે. $\frac{E^a}{2 b}\,J / s$ એ ચુંબકીય ક્ષેત્રમાં સંગ્રહ પામતી ઊર્જાનો મહત્તમ દર ધરાવે છે. $\frac{b}{a}$ નું મૂલ્ય .......... હશે.
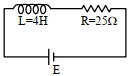

JEE MAIN 2023, Diffcult
c
\(E=\frac{1}{2} L I^2\)
\(E=\frac{1}{2} L I^2\)
Rate of energy storing \(=\frac{d E}{d t}=L I \frac{d I}{d t}\)
Now we Know for \(R-L\) circuit
\(I=\frac{E}{R}\left(1-e^{-t \frac{R}{L}}\right)\)
So \(\frac{d I}{d t}=\frac{E}{L} e^{-\frac{t R}{L}}\)
\(\frac{d E}{d t}=\frac{E^2}{R}\left(1-e^{-\frac{t R}{L}}\right)\left(e^{-t \frac{R}{L}}\right)\)
Time at which rate of power storing will be \(\max\)
\(t =\frac{L}{R \ln 2}\)
So \(\frac{d E}{d t}=\frac{E^2}{R}\left(1-\frac{1}{2}\right) \times \frac{1}{2}\)
\(\Rightarrow \frac{E^2}{4 R}=\frac{E^2}{100}=\frac{E^2}{2 \times 50}\)
\(a=2, b=50\)
So \(\frac{b}{a}=25\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionકઈ અવસ્થા દરમિયાન એડી પ્રવાહો જોવાં મળે છે ?
- 2View Solutionચુંબકીય ક્ષેત્રમાં ગતિ કરતાં ગૂંચળામાં પ્રેરિત થતો કુલ વિદ્યુતભાર કઇ બાબત પર આઘાર રાખે ?
- 3સ્ટેપડાઉન ટ્રાન્સફોર્મરને $2400\,V$ સાથે લગાવતા ગૌણ ગૂંચળામાં પ્રવાહ $80\,A$ છે,પ્રાથમિક અન ગૌણ ગૂંચળામાં આંટાની સંખ્યાનો ગુણોતર $20 : 1$ છે. જો કાર્યક્ષમતા $100\%$ હોય તો, પ્રાથમિક ગૂંચળામાં પ્રવાહ .....$amp$View Solution
- 4આકૃતિમાં દર્શાવ્યા અનુસાર એક ઇલેકટ્રોન સુરેખ પથ $xy$ પર ગતિ કરે છે. એક કોઈલ $abcd$ આ ઇલેકટ્રોનના માર્ગ ની નજીક છે. આ કોઇલમાં જો કોઇ પ્રવાહ પ્રેરિત થાય, તો તેની દિશા કઈ હશે?View Solution
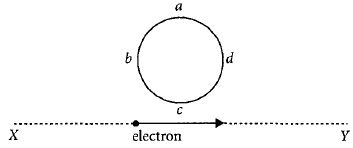
- 5$l$ બાજુવાળી ચોરસ લૂપને $L (L > l)$ બાજુવાળી મોટી ચોરસ લૂપને સમકેન્દ્રીય રીતે મૂકેલ છે,તો બંને વચ્ચે અનોન્યપ્રેરકત્વ કોના સપ્રમાણમાં હોય?View Solution
- 6$10 \mathrm{~cm}$ બાજુ અને $0.7 \Omega$ અવરોધની એક ચોરસ લૂપને પૂર્વ-પશ્રિમ સમતલમાં શિરોલંબ રાખેલી છે.$0.20$$T$ મૂલ્યના સમાન ચુંબકીય ક્ષેત્રને ઉત્તર-પૂર્વ દિશામાંના સમતલમાં રાખેલ છે. ચુંબકીય ક્ષેત્ર $1 S$ માં સ્થિર દરે ધટીને શૂન્ય થાય છે. તો પ્રેરિત emf નું મૂલ્ય $\sqrt{x} \times 10^{-3} V$ છે. તો $x$ નું મૂલ્ય________છે.View Solution
- 7$2.5 \mathrm{~m}$ લંબાઈ અને $2 \mathrm{~m}$ પહોળાઈની એક લંબચોરસ લૂપને $60^{\circ}$ ને કોણે $4 \mathrm{~T}$ મૂલ્યના ચુંબકીય ક્ષેત્રમાં મૂકેલી છે. ક્ષેત્રમાંથી $10 \mathrm{~s}$ માં લુપને દૂર કરવામાં આવે છે. આ સમય દરમિયાન પ્રેરિત થતું સરેરાશ $emf$____છે.View Solution
- 8ટ્રાન્સફોર્મરના ગૌણ ગૂંચળામાં $AC$ વોલ્ટેજ ઉત્પન્ન થવાનું કારણ નીચે પૈકી કયું છે?View Solution
- 9બે ઈન્ડક્ટરનો સમતુલ્ય પ્રેરણ $2.4\; H$ છે. જ્યારે તે સમાંતરમાં જોડેલ છે અને $10\; H$ છે જ્યારે તે શ્રેણીમાં જોડેલ છે. તો બંને પ્રેરણનો તફાવત (બે કોઈલ વચ્ચેનો અનોન્ય પ્રેરણા અવગણો)View Solution
- 10એક ગૂંચળામાં, પ્રવાહ $0.2 \mathrm{~s}$ માં $-2 \mathrm{~A}$ થી બદલાઈને $+2 \mathrm{~A}$ થાય છે. અને $0.1 \mathrm{~V}$ જેટલું પ્રેરિત $emf$ મળે છે. ગૂંચળાનું . . . . . હશે.View Solution
