આપેલ આકૃતિમાં કિરણ વિચલન વગર પસાર થતું હોય,તો નીચેનામાથી શું સાચું થાય?
Diffcult
Download our app for free and get started
d
(d) At \(B\)
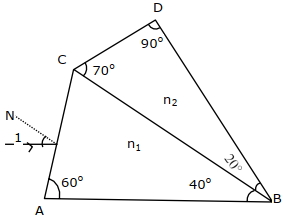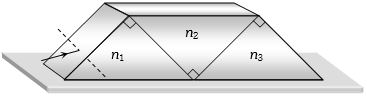
(d) At \(B\)
\(\sin i = {n_1}\sin {r_1}\) ==> \({\sin ^2}i = n_1^2{\sin ^2}{r_1}\) .... \((i)\)
At \(C\)
\({n_1}\sin (90 - {r_1}) = {n_2}\sin {r_2}\) ==>\(n_2^2{\sin ^2}{r_2} = n_1^2{\cos ^2}{r_1}\)....\((ii)\)
At \(D\)
\({n_2}\sin (90 - {r_2}) = {n_3}\sin {r_3}\)==>\(n_2^2{\cos ^2}{r_2} = n_3^2{\sin ^2}{r_3}\)....\((iii) \)
At \(E\)
\({n_3}\sin (90 - {r_3}) = (1)\sin (90 - 1)\)==>\({\cos ^2}i = n_3^2{\cos ^2}{r_3}\)....\((iv) \)
Adding \((i), (ii), (iii)\) and \((iv)\) we get \(1 + n_2^2 = n_1^2 + n_3^2\)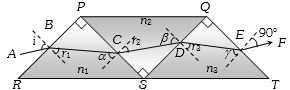
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
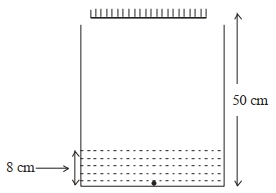
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે,એક સમતલીય અરીસાને પાણી ભરેલી ટાંકીના તળીયા $\left(\mu=\frac{4}{3}\right)$ થી $50\,cm$ ની ઊંચાઈએ સ્થિત કરવામાં આવે છે. ટાંકીમાં પાણીની ઊંચાઈ $8\,cm$ છે. એક નાના ગોળાને પાણીની ટાંકીના તળિયે મુકવામાં આવે છે. ટાંકીના તળિયાથી અરીસા દ્વારા મેળવાતા ગોળાના પ્રતિબિંબનું અંતર $.........\,cm$ છે.View Solution
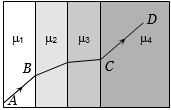
- 2પ્રકાશનું કિરણ $\mu_1, \mu_2, \mu_3$ અને $\mu_4$ વક્રીભવનાંકના ચાર પારદર્શક માધ્યમમાંથી આકૃતિમાં દર્શાવ્યા મુજબ પસાર થાય છે. બધી જ સપાટી એકબીજાને સમાંતર છે. જો નિર્ગમન કિરણ $CD$ આપાત કિરણ $AB$ ને સમાંતર છે, તો ......View Solution
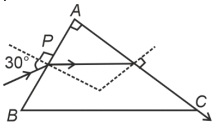
- 3આકૃતિમાં દર્શાવ્યા અનુસાર પ્રકાશ કિરણ કાટકોફા પ્રિજમના બિંદુ $P$ આગબ $30^{\circ}$ ના. આપાતકોણાથી દાખલ થાય છે. તે પ્રિજમના પાયા (બેજ) $B C$ મે સમાંતર ગતિ કરે છે અને $A C$ બાજુને સમાંતર નિર્ગમન પામે છે. પ્રિઝમનો વકીભવનાંક. . . . . . . . . થશે.View Solution
- 4View Solutionપ્રકાશનું પૂર્ણ આંતરિક પરાવર્તન કયારે થાય?
- 5ઘટ્ટ માધ્યમનો પાતળા માધ્યમની સાપેક્ષે વક્રીભવનાંક $n_{12}$ અને તેનો ક્રાંતિકકોણ $\theta_C$ છે. જ્યારે પ્રકાશ ઘટ્ટ માધ્યમમાંથી પાતળા માધ્યમમાં ગતિ કરતો હોય ત્યારે તે સપાટી પાસે $A$ ખૂણે આપત થાય છે, જેમાંથી થોડોક ભાગ પરાવર્તન પામે છે અને બીજો ભાગ વક્રીભવન પામે છે. પરાવર્તિતકિરણ અને વક્રીભૂતકિરણ વચ્ચેનો ખૂણો $90^o$ હોય તો આપતકોણ $A$ કેટલો હશે?View Solution
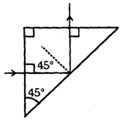
- 6$90°$ પ્રિઝમ કોણની એક સપાટી પર પ્રકાશનું કિરણ આપાત થાય છે અને તે કાચ હવાની આંતર સપાટી પર તેનું સંપૂર્ણ આંતરિક પરાવર્તન થયું છે. જો પરાવર્તન કોણ $45° $ હોય તો વક્રીભવનાંક n . . . . . .View Solution
- 7શરૂઆતમાં સમાંતર એવું નળાકાર કિરણજૂથ $\mu( I )=\mu_{0}+\mu_{2} I$ ધન વક્રીભવનાંકવાળા માધ્યમમાં પસાર થાય છે. અહી $\mu_{0}$ અને $\mu_{2}$ એ ધન અચળાંકો છે અને $I$ એ કિરણજૂથની તીવ્રતા છે. ત્રિજ્યામાં વધારા સાથે કિરણજૂથની તીવ્રતામાં ઘટાડો થાય છે.View Solution
આ કિરણજૂથ દ્વારા રચાતા તરંગઅગ્રનો શરૂઆતનો આકાર કેવો હશે?
- 8View Solutionબર્હિગોળ લેન્સ ત્રણ જુદાં જુદાં દ્રવ્યમાંથી બનાવેલ હોય,તો કેટલા પ્રતિબિંબ મળશે?
- 9$20 \;cm$ અને $25\; cm$ કેન્દ્રલંબાઈ ધરાવતા બે પાતળા બહિર્ગોળ લેન્સને સંપર્કમાં મૂકવામાં આવે તો તેમણે સમતુલ્ય પાવર કેટલો મળે?View Solution
- 10$n_{1}$ વક્રીભવનાંક ધરાવતા એક પ્રિઝમને $n_{2}$ વક્રીભવનાંક ધરાવતા બીજા પ્રિઝમ સાથે (આકૃતિમાં દર્શાવ્યા મુજબ) ચોટાડવામાં આવ્યા છે. $n_{1}$ અને $n_{2}$ એ $\lambda$ પર નીચે આપેલ સૂત્ર મુજબ આધાર રાખે છે, જ્યાં $\lambda$ એ પ્રકાશની તરંગલંબાઈ છે.View Solution
${n}_{1}=1.2+\frac{10.8 \times 10^{-14}}{\lambda^{2}}$ અને ${n}_{2}=1.45+\frac{1.8 \times 10^{-14}}{\lambda^{2}}$
$BC$ આંતરપૃષ્ઠ ઉપર કોઈ પણ ખૂણે આપાત કિરણ કે જે આંતર પૃષ્ઠ આગળ વાંકું વળ્યા વગર પસાર થઈ જાય તે તરંગલંબાઈ $....\,nm$ હશે.
