આપેલ આલેખ વેગ વિરુદ્ધ સ્થાનાંતર નો વક્ર દર્શાવે છે.તો નીચેનામાથી કયો આલેખ પ્રવેગ વિરુદ્ધ સ્થાનાંતર ના વક્ર માટે સાચો છે?
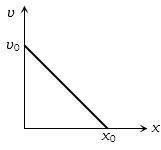

IIT 2005, Diffcult
a
(a) Given line have positive intercept but negative slope. So its equation can be written as
(a) Given line have positive intercept but negative slope. So its equation can be written as
$v = - mx + {v_0}$…..(i) [where $m = \tan \theta = \frac{{{v_0}}}{{{x_0}}}$]
By differentiating with respect to time we get $\frac{{dv}}{{dt}} = - m\frac{{dx}}{{dt}} = - mv$
Now substituting the value of $v$ from eq. (i) we get $\frac{{dv}}{{dt}} = - m[ - mx + {v_0}] = {m^2}x - m{v_0}$
$\therefore a = {m^2}x - m{v_0}$
i.e. the graph between $a$ and $x$ should have positive slope but negative intercept on $a-$axis. So graph $(a) $ is correct.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ટ્રેન વિરામસ્થિતિમાંથી પ્રથમ નિયમિત પ્રવેગથી $t$ સમયમાં $80 \mathrm{~km} / \mathrm{h}$ ની ઝડપ પ્રાપ્ત કરે છે ત્યારબાદ તે $3 t$ સમય માટે અચળ ઝડપથી ગતિ કરે છે. આ સમયગાળાની મુસાફરી દરમિયાન ટ્રેનની સરેસાશ ઝડપ ($km/h$માં). . . . . .હશે.View Solution
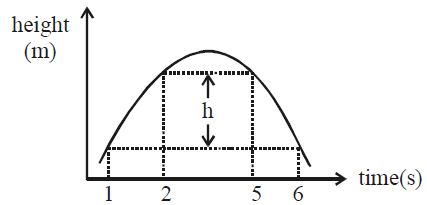
- 2એક દડાને ઉપર તરફ ફેંકવામાં આવે છે. તેની ઊંચાઈ નીચે મુજબ સમય સાથે બદલાય છે. ગુરુત્વ પ્રવેગ $7.5\ m/s^2$ હોય તો ઊંચાઈ $h$ એ કેટલા $..........m$ હશે?View Solution
- 3એક ટાવરની ટોચ પરથી ઝડ૫ $u$ સાથે ઉપરથી ફેકવામાં આવે પથ્થર વેગ $4 u$ સાથે જમીન પર પહોંચે છે. ટાવરની ઊંચાઈ ક્ટલી હશે?View Solution
- 4એક બોલને નદી ઉપર $122.5 \,m$ ના પુલ પરથી ફેકવામાં આવ્યો છે. પ્રથમ બોલ $2$ સેકન્ડ માટે ગતિ કરે છે પછી, બીજો બોલ તેના પડ્યા પછી તરત જ ફેકવામાં આવે છે. બીજા બોલનો પ્રારિભિક વેગ કે જેથી બંને એક જ સમયે પાણીમાં પડે તે ......... $m/s$ છે?View Solution
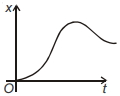
- 5કણનો સ્થાનાંતર $(x)$ -સમય $(t)$ નો આલેખ આકૃતિમાં દર્શાવવામાં આવ્યો છે. નીચેનામાંનું કયું સાયું છે?View Solution
- 6એક કાર કુલ અંતરના $2/5^{th}$ માં ભાગનું અંતર $v_1$ ઝડપથી અને $3/5^{th}$ માં ભાગનું અંતર $v_2$ ઝડપથી કાપતો હોય,તો સરેરાશ ઝડપ કેટલી થાય?View Solution
- 7$120\, m$ લાંબી ટ્રેન $A$ કોઈ એક દિશામાં $20 \,m/s$ ના વેગથી ગતિ કરે છે. બીજી $130\, m$ લાંબી ટ્રેન $B$ તેની વિરુદ્ધ દિશામાં $30\, m/s$ ના વેગથી ગતિ કરે તેને પ્રથમ ટ્રેન $A$ ને પસાર કરતાં કેટલો સમય લાગશે?View Solution
- 8એક કણ ઉદ્ગમ બિંદુથી સ્થિર સ્થિતિમાં $6 m/s^2$ ના પ્રવેગથી $x$ દિશામાં અને $8 m/s^2$ ના પ્રવેગથી $y$ દિશામાં ગતિ કરતો હોય,તો $4 sec$ પછી તેણે કેટલા........$m$ સ્થાનાંતર કર્યું હશે?View Solution
- 9બે ટ્રેન સમાન ટ્રેક પર $40 \,m/s$ ની ઝડપથી એકબીજા તરફ ગતિ કરે છે,જયારે બંને ટ્રેન $2 \,km$ અંતરે હોય,ત્યારે બંને ટ્રેનમાં એકસમાન પ્રતિપ્રવેગ ઉત્પન્ન કરવામાં આવે છે.અથડામણ અટકાવવા માટે પ્રતિ પ્રવેગનું મૂલ્ય કેટલા.........$m/{s^2}$ હોવું જોઈએ?View Solution
- 10એક કણનું સ્થાનાંતર $x$ સમય $t$ સાથે $x = a{e^{ - \alpha \,t}} + b{e^{\beta \,t}}$ મુજબ બદલાય છે, જ્યાં $a ,b,\alpha$ અને $\beta$ એ ધન અચળાંક છે. કણનો વેગ ........View Solution
