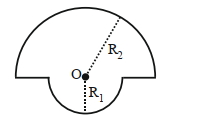
આપેલ પરિપથમાં કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?

Medium
b
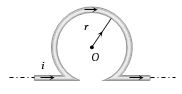
(b)The given shape is equivalent to the following diagram The field at \(O\) due to straight part of conductor is \({B_1} = \frac{{{\mu _o}}}{{4\pi }}.\frac{{2i}}{r} \odot \). The field at \(O\) due to circular coil is \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\pi i}}{r} \otimes \). Both fields will act in the opposite direction, hence the total field at \(O\). i.e. \(B = {B_2} - {B_1} = \left( {\frac{{{\mu _o}}}{{4\pi }}} \right) \times (\pi - 1)\frac{{2i}}{r} = \frac{{{\mu _o}}}{{4\pi }}.\frac{{2i}}{r}(\pi - 1)\)
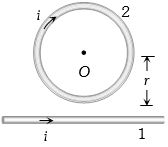
(b)The given shape is equivalent to the following diagram The field at \(O\) due to straight part of conductor is \({B_1} = \frac{{{\mu _o}}}{{4\pi }}.\frac{{2i}}{r} \odot \). The field at \(O\) due to circular coil is \({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\pi i}}{r} \otimes \). Both fields will act in the opposite direction, hence the total field at \(O\). i.e. \(B = {B_2} - {B_1} = \left( {\frac{{{\mu _o}}}{{4\pi }}} \right) \times (\pi - 1)\frac{{2i}}{r} = \frac{{{\mu _o}}}{{4\pi }}.\frac{{2i}}{r}(\pi - 1)\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે અતિ લાંબા સુરેખ વાહક તારો વચ્ચેનું લંબઅંતર $2d$ છે.તેમનામાંથી સમાન મૂલ્યના સ્થિર પ્રવાહો પુસ્તકના પાનામાંથી બહાર આવતી દિશામાં વહે છે. $XX’$ સુરેખા પર,ચુંબકીય ક્ષેત્ર $\vec B$ માં થતો ફેરફાર નીચેનામાંથી કયા આલેખ દ્રારા રજૂ કરી શકાય?View Solution
- 2$m$ દળ અને $q$ વિદ્યુતભાર ધરાવતા ઇલેક્ટ્રોન $B$ ચુંબકીયક્ષેત્રમાં $r$ ત્રિજ્યામાં વર્તુળમય ગતિ કરે છે,જો વેગ બમણો અને ચુંબકીયક્ષેત્ર અડધું થાય તો વર્તુળમયગતિની ત્રિજ્યા .....View Solution
- 3સૂચિ $I$ અને સૂચિ $II$ને મેળવોઃView Solution
આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરોઃ

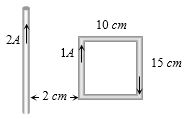
- 4View Solutionઆપેલ આકૃતિ માં રહેલ લૂપ પર કેટલું બળ લાગતું હશે?
- 5એક વિસ્તારમાં સમાન વિદ્યુતક્ષેત્ર $\vec E$ અને સમાન ચુંબકીયક્ષેત્ર $\vec B$ એક જ દિશામાં પ્રવર્તે છે.એક ઇલેકટ્રોન આ ક્ષેત્રેની દિશામાં ચોકકસ વેગથી દાખલ થાય છે,તો...View Solution
- 6$X$ અક્ષ અને $Y$ - અક્ષ પર મૂકેલા બે અનંત લંબાઇના તારમાંથી $8A$ અને $6A$ પ્રવાહ પસાર થાય છે,તો $ P\,(0,\,0,\,d)\,m $ બિંદુ પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 7અચળ વેગ સાથે ગતિ કરતો પ્રોટોન અવકાશના વિસ્તારમાંથી તેના વેગમાં ફેરફાર થયા વગર, પસાર થાય છે. જો $E$ અને $B$ નીચેનામાંથી ક્યું હોઈ શકે ?View Solution
- 8બે લાંબા સીધા તારોને $x$-અક્ષ અને $y$-અક્ષ પર મૂકવામાં આવ્યા છે.તે અનુક્રમે $I_1$ અને $I_2$ વિદ્યુતપ્રવાહ ધરાવે છે. તેમના વડે રચતા વિદ્યુતક્ષેત્રમાં શૂન્ય ચુંબકીય પ્રેરણના સ્થાનનું સમીકરણ કયું છે?View Solution
- 9સમાન ગતિઊર્જા ધરાવતા બે વિદ્યુતભારિત કણો ગતિની દિશાને લંબરૂપે રહેલા નિયમિત ચુંબકીય ક્ષેત્રમાંથી પસાર કરાવવામાં આવે છે. જે તેમના વર્તુળાકાર પથોની ત્રિજ્યાઓનો ગુણોત્તર $6: 5$ હોય અને તેમના દળોનો ગુણોત્તર $9: 4$ હોય, તો તેમના પરના વીજભારોનો ગુણોત્તર $......$ થશે.View Solution
- 10આકૃતિમાં દર્શાંવ્યા અનુસાર, $\mathrm{I}=4 \mathrm{~A}$ નો પ્રવાહ ધરાવતી અને $\mathrm{R}_1=2 \pi$ મીટર અને $\mathrm{R}_2=4 \pi$ મીટરની ત્રિજ્યા ધરાવતા બે અર્ધવર્તુળાકાર ગાળાના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર $\alpha \times 10^{-7}$ ટેસ્લા છે. (દરેક ભાગ માટે કેન્દ્ર $\mathrm{O}$ છે.)View Solution