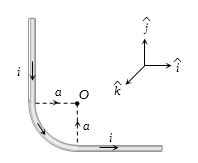
આપેલ પરિપથમાં $O$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?

Diffcult
d
(d) The field at \(O\) due to \(AB\) is \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\hat k\) and that due to \(DE\) is also \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\hat k\).
However the field due to \(BCD\) is \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\left( {\frac{\pi }{2}} \right)\,\hat k\).
Thus the total field at \(O\) is \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\left( {2 + \frac{\pi }{2}} \right)\,\hat k\)
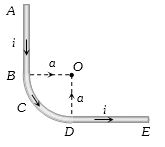
(d) The field at \(O\) due to \(AB\) is \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\hat k\) and that due to \(DE\) is also \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\hat k\).
However the field due to \(BCD\) is \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\left( {\frac{\pi }{2}} \right)\,\hat k\).
Thus the total field at \(O\) is \(\frac{{{\mu _0}}}{{4\pi }}.\frac{i}{a}\left( {2 + \frac{\pi }{2}} \right)\,\hat k\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ચલિત ગૂંચળાના ગેલ્વેનોમીટર માટે જ્યારે $10\,mA$ પ્રવાહ પસાર થાય ત્યારે ગૂંચળાનું સ્થાનાંતર $0.05$ રેડિયન થાય છે. જો લટકાવેલ તારનો વળ અચળાંક $4.0 \times 10^{-5}\,N\,m\,rad ^{-1}$, ચુંબકીય ક્ષેત્ર $0.01\,T$ અને ગૂંચળાના આંટાની સંખ્યા $200$ હોય, તો પ્રત્યેક આંટાનું ક્ષેત્રફળ ($cm ^2$ માં) $...........$View Solution
- 2$15 \,cm$ જેટલી સરેરાશ ત્રિજ્યાની રોલેન્ડ $(Rowland)$ રીંગના, $800$ જેટલી સાપેક્ષ પરમિએબિલીટી ધરાવતા કોર પર તારના $3500$ આંટા વિંટાળવામાં આવેલ છે. $1.2\, A$ જેટલા મેગ્નેટાઇઝીંગ વિદ્યુતપ્રવાહ માટે કોરમાં ચુંબકીય ક્ષેત્ર $B$ કેટલું હશે?View Solution
- 3એક ચોરસ લૂપ $ABCD$ માંથી $i $ પ્રવાહ પસાર થાય છે, તેને $I$ પ્રવાહધારીત રેખીય વાહકતાર $XY$ ની નજીક મૂકેલ છે, લૂપ પર પરિણામી બળ કેટલું લાગશે?View Solution
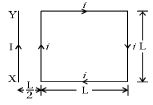
- 4$i$ પ્રવાહવાળા $d\vec l$ લંબાઇના ખંડથી $\vec r$ અંતરે ચુંબકીયક્ષેત્ર $d\overrightarrow B$ કેટલું થાય?View Solution
- 5એક ચલિત ગૂંચળાવાળા ગેલ્વેનોમીમટરના ગૂંચળાને $200 \mu \mathrm{A}$ ના પ્રવાહ દ્વારા $60^{\circ}$ કોણે આવર્તિત કરવામાં આવે છે. $\frac{\pi}{10}$ રેડિયન જેટલું પરિભ્રમણ કરવવા માટેનો પ્રવાહ______છે.View Solution
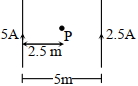
- 6આપેલી આકૃતિમાં રહેલ બિંદુ $P$ પરનું ચુંબકીય ક્ષેત્ર કેટલું થશે?View Solution
- 7તારમાં $ i $ પ્રવાહ ઘન $X-$ દિશામા પસાર થાય છે.ચુંબકીયક્ષેત્ર $\overrightarrow B = {B_0}$ ($\hat i + \hat j + \hat k)$ $T$ છે.તો તેના પર કેટલું બળ લાગશે?View Solution
- 8બે તાર $AOB$ અને $COD$ ને લંબ રાખીને તેમાંથી $ {i_1} $ અને $ {i_2} $ પ્રવાહ પસાર કરવામાં આવે છે.તો બિંદુ $O$ થી $ABCD$ સમતલને લંબ $a$ અંતરે બિંદુ $P$ આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
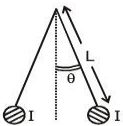
- 9$I$ વિદ્યુતપ્રવાહ ધરાવતા બે પાતળા લાંબા વિદ્યુતભારિત તારને $L$ લંબાઇની અવાહક દોરીઓ વડે ટેકવવામાં આવ્યા છે,કે જેથી તેઓ આકૃતિમાં દર્શાવ્યા મુજબ સંતુલન સ્થિતિમાં રહે.અત્રે દોરીઓ ઊર્ધ્વદિશા સાથે ‘$\theta '$ કોણ બનાવે છે.જો તાર માટે એકમ લંબાઇ દીઠ સરેરાશ $‘λ’$ હોય,તો પ્રવાહ $I$ નું મૂલ્ય _______. ( $ g$ $=$ ગુરુત્વપ્રવેગ)View Solution
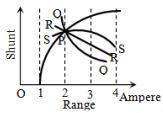
- 10એમીટર શંટ વગર $1$ $A$ ની રેન્જ ધરાવે છે. જુદા જુદા શંટ અવરોધનો ઉપયોગ કરીને એેમીટરની રેન્જમાં ફેરફાર કરી શકાય. તો શંટ અવરોધ અને રેન્જ વચ્ચેનો આલેખ કયો સ્વભાવ ધરાવે છે ?View Solution