\({\omega _2} = {\omega _1}\, - \,\,\alpha t\,\,\,\)
\(\therefore \,\,0\,\, = \,\,2\pi n\, - \,\,\alpha t\,\, \Rightarrow \,\,t\,\, = \,\,\frac{{2\pi n}}{\alpha }\,\, = \,\,\frac{{2\pi \, \times \,240}}{{\pi \,\, \times \,\,60}}\,\, = \,\,8\,\,s\)
હવે, \(\begin{gathered}
\because \,\,\omega _2^2\,\, = \,\,\,\omega _1^2\,\, - \,\,2\alpha \,\theta \,\,\,\,\,\,\,\therefore \,\,0\,\, = \,\,\omega _1^2\,\, - \,\,2\,\alpha \,\theta \hfill \\
\Rightarrow \,\,\,\theta \,\, = \,\,\,\frac{{\omega _1^2}}{{2\alpha }}\,\, = \,\,\,\frac{{4{\pi ^2}{n^2}}}{{2\alpha }}\,\, = \,\,\,\frac{{4{\pi ^2}}}{{2\pi }}\,\, \times \,\,\,{\left( {\frac{{240}}{{60}}} \right)^2}\, = \,\,\,32\,\pi \hfill \\
\end{gathered} \)
\(\, \Rightarrow \) ભ્રમણ ની સંખ્યા \( = \,\, \frac{\theta }{{2\pi }}\,\, = \,\,\,\frac{{32\pi }}{{2\pi }}\,\, = \,\,\,16\)
Download our appand get started for free
Similar Questions
- 1$M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીની કોણીય ઝડપ $\omega_{1}$ છે. બીજી $\frac{ R }{2}$ ત્રિજ્યા અને $M$ દળ ધરાવતી તકતી તેના પર મુક્તા નવી કોણીય ઝડપ $\omega_{2}$ છે.શરૂઆતની ઊર્જાનો વ્યય થાય તો $p=.......$View Solution
- 2$I_1=4 \mathrm{~kg} \mathrm{~m}^2$ અને $I_2=2 \mathrm{~kg} \mathrm{~m}^2$ જેટલી જડત્વની ચાકમાત્રા ધરાવતી બે તકતી, તેઓની કેન્દ્રીય અક્ષો અને તક્તિઓન લંબ હોય તને અનુલક્ષીને અનુક્રમે $10 \mathrm{rad} / \mathrm{s}$ અને $4 \mathrm{rad} / \mathrm{s}$ ની કોણીય ઝડપથી ભ્રમણ કરે છે જેને તેઓની પરિભ્રમણ અક્ષો એકબીજા પર સંપાત થાય તે રીતે સામસામે એકબીજાના સંપર્કમાં લાવવામાં આવે છે. આ પ્રક્રિયા દરમ્યાન ગતિ ઊર્જામાં થતો ધટાડો__________$\mathrm{J}$છે.View Solution
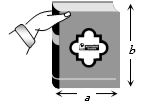
- 3એક માણસ એક બુક ને આકૃતિમાં દર્શાવ્યા મુજબ પકડે છે (ધારો કે બુકને બુકના ખૂણે પકડેલી છે ) જો બુકનો વજન $W$ હોય તો માણસ દ્વારા બુક પર લાગતું ટોર્ક કેટલું થાય $?$View Solution
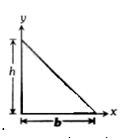
- 4View Solutionઆકૃતિમાં દર્શાવેલ ત્રિકોણના દ્રવ્યમાન-કેન્દ્રના યામ ....... .
- 5સમાંગ (નિયમિત) પાતળા સળિયાની તેના એક છેડામાંથી પસાર થતી લંબ અક્ષને અનુલક્ષીને જડત્વની ચાક માત્રા $I_{1}$ છે. આ જ સળિયાને વાળીને રીગ બનાવવામાં આવ છે. હવે તેની વ્યાસને અનુલક્ષીને જડત્વની ચાકમાત્રા $I_{2}$ થાય છે. જો $\frac{I_{1}}{I_{2}}$ એ $\frac{x \pi^{2}}{3}$, હોય તો $x$ નું મૂલ્ય ........... હશે.View Solution
- 6$M$ દળના અને $r$ ત્રિજ્યાની નિયમિત અર્ધ-વર્તૂળાકાર તકતીમાં કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ રેખા પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
- 7ચાકમાત્રા ના સિદ્ધાંતો પર કામ કરતાં ભૌતિક ત્રાજવા માં, જ્યારે ડાબા પલ્લાંમાં $5\, mg$ વજન મૂકવામાં આવે છે ત્યારે ત્રાજવાની દાંડી સમક્ષિતિજ થાય છે. બંને ખાલી પલ્લાં સમાન દળ ના છે. તો નીચેનામાથી શું કહી શકાય ?View Solution
- 8$m$ દળનો એક કણ એ વેગ $v$ થી સમક્ષિતિજ સાથે $30^{\circ}$ નો ખૂણો બનાવીને પ્રક્ષિપ્ત ગતિ કરે છે. આ કણ જ્યારે મહત્તમ ઉંચાઈ પ્રાપ્ત કરે તે સમયે, ગતિની શરૂઆતના બિંદુની સાપેક્ષે કણના કોણીય વેગમાનનું મૂલ્ય ફેટલું હશે?View Solution
- 9$1.5 \,m$ લાંબા એક સળિયાના $A$ અને $B$ છેડાઓ પર અનુક્રમે $20 \,N$ અને $30 N$ ના એેક જ જેવા સમાંતર બળો લગાડવામાં આવે છે. તો આ બળોનું પરિણામી બળ ક્યા બિંદુ પર લાગતું હશે?View Solution
- 10એક $ m$ દળ, $r $ જેટલી ત્રિજ્યા અને $\omega_0$ જેટલી કોણીય આવૃત્તિ ધરાવતી રિંગને ખરબચડી સપાટી પર રાખેલ છે. રિંગના કેન્દ્રનો પ્રારંભિક વેગ શૂન્ય છે. જ્યારે રિંગ સરકવાનું બંધ કરે ત્યારે તેના કેન્દ્રનો વેગ કેટલો હશે ?View Solution
