અંતર્ગોળ અરીસો સમક્ષિતિજ ટેબલ પર મૂકેલો છે જેથી અક્ષ શિરોલંબ ઉર્ધ્વ દિશામાં છે. ધારો કે $O$ એ અરીસાનો ધ્રુવ અને $C$ એ વક્રતા કેન્દ્ર છે. બિંદુવત્ પદાર્થ $C$ પર મૂકેલો છે. તેની વાસ્તવિક પ્રતિબિંબ $C$ પર મળે છે. જો હવે અરીસામાં પાણી ભરવામાં આવે ત્યારે પ્રતિબિંબ . . . . . .
Easy
d
consider the arrangement to be combination of plano convex lens and a concave mirror
let \(R\) be radius of curvature
\(f_{\text {leass }}=\frac{R}{2}\) and \(f_{\text {mirror }}=\frac{R}{2}\)
first image is formed by lens
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}+\frac{1}{R}=\frac{2}{R}\)
\(v=R\)
now this serves as virtual image for mirror
\(u=+R\)
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}+\frac{1}{R}=\frac{-2}{R}\)
\(v=\frac{-R}{3}\)
this again serves as virtual image for the lens
\(u=\frac{R}{3}\)
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}-\frac{3}{R}=\frac{2}{R}\)
\(v=\frac{R}{5}\)
hence the image is real and formed between \(O\) and \(C\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$X-Y$ સમતલને બે પારદર્શક માધ્યમો $M_1$ અને $M_2$ ને જોડતી સીમા (સપાટી) તરીકે લઈ શકાય. $M_1$ ને $Z \geqslant 0$ માટે $\sqrt{2}$ જેટલો વક્રીભવનાંક અને $M _2$ ને $Z < 0$ માટે $\sqrt{3}$ જેટલો વક્રીભવનાંક છે. $M _1$ માં $\overrightarrow{ P }=4 \sqrt{3} \hat{i}-3 \sqrt{3} \hat{j}-5 \hat{k}$ સદિશ વડે અપાતો પ્રકાશ બે માધ્યમોની છૂટી પાડતી સપાટી ઉપર આપાત કરવામાં આવે છે. $M_1$ માં આપાતકોણ અને $M_2$ માં વક્રીભૂતકોણ વરચેચેનો તફાવત $.................$ ડીગ્રી થશે.View Solution
- 2View Solutionએસ્ટીગ્મેટીઝમ નિવારવા માટે કયા લેન્સ પહેરવા પડે?
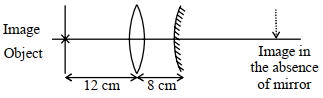
- 3એક વસ્તુને બહિર્ગોળ લેન્સથી $12 \,{cm}$ અંતરે મૂકેલો છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે $15 \,{cm}$ કેન્દ્રલંબાઈ ધરાવતા બહિર્ગોળ અરિસાને લેન્સની બીજી બાજુ $8 \,{cm}$ અંતરે મૂકેલો છે. વસ્તુનું પ્રતિબિંબ વસ્તુ પાસે જ મળે છે. જ્યારે બહિર્ગોળ અરિસાને દૂર કરવામાં આવે ત્યારે વાસ્તવિક અને ઊલટું પ્રતિબિંબ મળે છે. તો વસ્તુથી આ પ્રતિબિંબ કેટલા $(cm)$ દૂર બનશે?View Solution
- 4ખાલી બીકરમાં સિકકો પડેલ છે,તે માઇક્રોસ્કોપ દ્વારા ફોકસ કરેલ છે,તેમાં $10 \,cm$ ઊંચાઇ સુધી પાણી ભરતાં તેને ફરીથી ફોકસ કરવા માટે માઇક્રોસ્કોપને કેટલું ખસેડવું પડે?View Solution
- 5$60\; \mathrm{cm}$ ટ્યૂબલંબાઈ ધરાવતા ટેલિસ્કોપની મોટવણી $5$ છે તો તેના નેત્રકાચની કેન્દ્રલંબાઈ કેટલા ......$cm$ હશે?View Solution
- 6$10cm$ કેન્દ્રલંબાઇ ધરાવતો અંર્તગોળ લેન્સ અને $30cm$ કેન્દ્રલંબાઇ ધરાવતો બર્હિગોળ લેન્સ અમુક અંતરે મૂકેલા છે. સમાંતર કિરણો બર્હિગોળ લેન્સ પર આપાત કરતાં અંર્તગોળ લેન્સમાંથી બહાર આવતા કિરણો પણ સમાંતર હોય,તો બંને લેન્સ વચ્ચેનું અંતર કેટલા.......$cm$ હશે?View Solution
- 7સમતલ અરીસો તમારા તરફ $10\,cm/sec$ ના વેગથી આવતો હોય,તો તમારા પ્રતિબિંબનો વેગ કેટલા ......$cm/sec$ થાય?View Solution
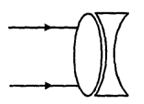
- 8આકૃતિમાં દર્શાવ્યા મુજબ, $50\, cm$ કેન્દ્રલંબાઈનો અંતર્ગોળ લેન્સ અને $25\,\, cm$ કેન્દ્રલંબાઈ નો બહિર્ગોળ લેન્સને એકબીજાના સંપર્કમાં રાખેલા છે. હવે જો સમાંતર પ્રકાશનું પૂંજ તંત્ર પર આપાત થાય તો તે કેવી રીતે નિર્ગમન પામશે?View Solution
- 9પાણીમાંથી લીલો પ્રકાશ હવા-પાણી આંતરપૃષ્ઠ પર ક્રાંતિકોણ $\theta $ એ આપાત થાય છે.સાચું વિધાન પસંદ કરો.View Solution
- 10પ્રવાહી ભરેલા પ્રિઝમ માટે લઘુત્તમ વિચલનકોણ $30^o $ અને વક્રીભૂતકોણ $30^o $ હોય,તો પ્રવાહીનો વક્રીભવનાંક કેટલો હશે?View Solution
