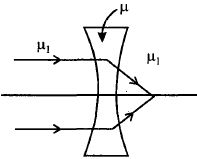
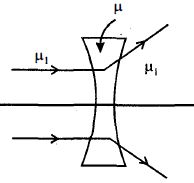
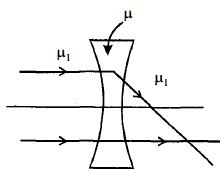
અંતર્ગોળ લેન્સના દ્રવ્યનો વક્રીભવનાંક $\mu $ છે. તેને $\mu _1$ વક્રીભવનાંક ધરાવતા માધ્યમમાં ડુબાડવામાં આવે છે. જો લેન્સ પર સમાંતર કિરણો આપાત કરવામાં આવે અને $\mu _1 > \mu $ હોય તો બહાર આવતા કિરણનો પથ કેવો હશે?
JEE MAIN 2014, Diffcult
a
If a lens of refractive index \(\mu\) is immersed in a medium of refractive index \(\mu_{1}\), then its focal length in medium is given by
If a lens of refractive index \(\mu\) is immersed in a medium of refractive index \(\mu_{1}\), then its focal length in medium is given by
\(\frac{1}{{{f_m}}} = {(_m}{\mu _l} - 1)\left( {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right)\)
If \(f_{a}\) is the focal length of lens in air, then
\(\frac{1}{{{f_a}}} = {(_a}{\mu _l} - 1)\left( {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right)\)
\( \Rightarrow \frac{{{f_m}}}{{{f_a}}} = \,\frac{{{(_a}{\mu _l} - 1)}}{{{(_m}{\mu _l} - 1)}}\)
If \(\mu_{l}>\mu,\) then \(f_{m}\) and \(f_{a}\) have opposite signs and the nature of lenschanges i.e. a convex lens diverges the light rays and concave lens converges the light rays. Thus given option \((a)\) is correct.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ખગોળીય દૂરબીનના વસ્તુકાચની કેન્દ્રલંબાઈ $100\, cm$ અને નેત્રકાચની કેન્દ્રલંબાઈ $5\, cm$ છે. તારાનું અંતિમ પ્રતિબિંબ નેત્રકાચથી $25\, cm$ અંતરે જોવામાં આવે છે. દૂરબીનનો મોટવણી પાવર કેટલો છે ?View Solution
- 2અરીસામાં સમય $3:25$ હોય,તો સાચો સમય કેટલો હશે?View Solution
- 3ટેલિસ્કોપનો મેગ્નિફિકેશન પાવર $9$ અને લેન્સ વચ્ચેનું અંતર $20\, cm$ છે તો ઘટક લેન્સની કેન્દ્રલંબાઈ શું થશે?View Solution
- 4એક માણસ $11\,\, km$ અંતરે રહેલાં બે થાંભલા સ્પષ્ટ જોઈ શકે છે. તો થાંભલા વચ્ચેનું ન્યૂનત્તમ અંતર ........$ m$ હોવું જોઈએ?View Solution
- 5એક કાંચનો વક્રીભવનાંક $1.5$ છે, શૂન્યાવકાશમાંથી પસાર થતાં પ્રકાશના કિરણની તંગલંબાઇ $6000\;\mathring A$ છે જે આ કાંચમાંથી પસાર થાય ત્યારે તેની તરંગલંબાઈ કેટલા $\mathring A$ હશે?View Solution
- 6પદાર્થ પ્રારંભમાં સમતલ અરીસાથી $100\,\, cm$ દૂર છે. જો અરીસો પદાર્થ તરફ $10\,\, cm/s$ તરફ ગતિ કરે છે. ત્યાર બાદ $6\,\, s$ બાદ પ્રદાર્થ અને પ્રતિબિંબ વચ્ચેનું અંતર .......$cm$ હશે.View Solution
- 7$20\,cm$ કેન્દ્ર લંબાઈના બે બહિર્ગોળ લેન્સને સમઅક્ષીય રીતે એકબીજાથી $60\; cm$ દૂર મુકેલા છે. દૂરના અંતરે રહેલી વસ્તુનું સંયોજન વડે રચાતું પ્રતિબિંબ પ્રથમ લેન્સથી .......... $cm$ અંતરે હશે.View Solution
- 8$60^\circ$ના ખૂણે રાખેલા સમતલ અરીસા વચ્ચે લેમ્પ મૂકતાં તેના કેટલા પ્રતિબિંબ મળશે?View Solution
- 9શ્વેત પ્રકાશને $5°$ કોણના પ્રિઝમ માંથી પસાર કરેલ છે. જો લાલ અને વાદળી રંગોના વક્રીભવનાંક અનુક્રમે $1.641$ અને $1.659$ હોય, તો તેમની વચ્ચેના વિભાજન કોણ..... હશે.View Solution
- 10$15\, cm$ જેટલી કેન્દ્રલંબાઈ ધરાવતા અને $1.5$ જેટલો વક્રીભવનાંક ધરાવતા બે સમાન લેન્સોને એક્બીના સંપર્કમાં રાખવામાં આવેલા છે. બે લેન્સો વચ્વચેની જગ્યામાં $1.25$ વક્રીભવનાંક ધરાવતું પ્રવાહી ભરવામાં આવે છે. તો આ સંચોજનની કેન્દ્રલંબાઈ .....$cm$ હશે.View Solution